Рациональные дроби. Рациональной дробью 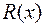 называется дробь, числителем и знаменателем которой являются многочлены, т. е. всякая дробь вида
называется дробь, числителем и знаменателем которой являются многочлены, т. е. всякая дробь вида
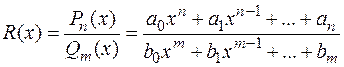
Если степень многочлена в числителе больше или равна степени многочлена в знаменателе (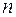 r
r 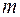 ), то дробь называется неправильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе (
), то дробь называется неправильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе (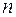 <
< 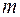 ), то дробь называется правильной.
), то дробь называется правильной.
Например,
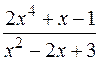 ,
, 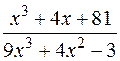 — неправильные дроби,
— неправильные дроби,
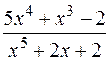 — правильная дробь.
— правильная дробь.
Всякую неправильную рациональную дробь (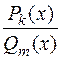 ,
, 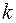 r
r 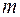 ) можно представить в виде суммы многочлена (целой части
) можно представить в виде суммы многочлена (целой части 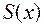 ) и правильной рациональной дроби(
) и правильной рациональной дроби(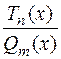 ,
, 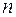 <
< 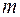 ):
):
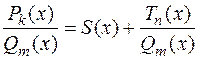
Это представление достигается путем деления числителя на знаменатель по правилу деления многочленов.
Пример. 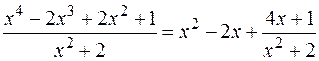 ,
,
так как
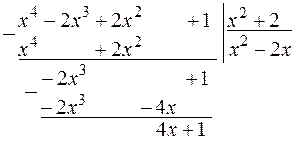
Пример. 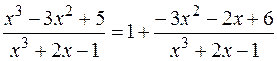 ,
,
так как
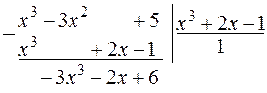
Так как интегрирование многочлена не представляет затруднений, то интегрирование рациональных дробей сводится к интегрированию правильных рациональных дробей.
Интегрирование простейших рациональных дробей. Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) 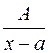 ,
,
2) 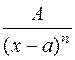 ,
, 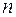 r
r 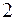 ,
,
3) 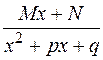 ,
,
4) 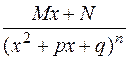 ,
, 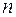 r
r 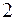 .
.
Здесь 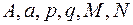 — действительные числа, а трехчлен не имеет действительных корней.
— действительные числа, а трехчлен не имеет действительных корней.
Простейшие дроби первого и второго типов интегрируются непосредственно с помощью основных правил интегрального исчисления:
1) 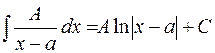 ,
,
2) 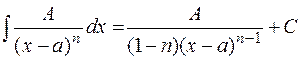 ,
,
3) Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов.
Пример. Найти 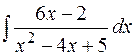 .
.
 2015-06-04
2015-06-04 787
787








