Решение. 4) Интегрирование простейшей рациональной дроби четвертого типа с помощью замены приводится к рекуррентной формуле

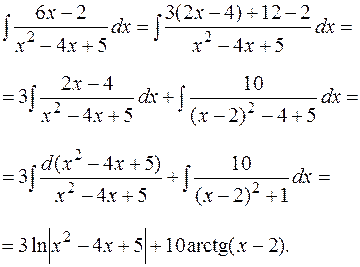
4) Интегрирование простейшей рациональной дроби четвертого типа с помощью замены 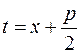приводится к рекуррентной формуле.

Разложение рациональной дроби на простейшие дроби. Всякую правильную рациональную дробь 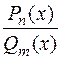можно представить в виде суммы конечного числа простейших рациональных дробей первого — четвертого типов. Для разложения 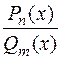на простей­шие дроби необходимо разложить знаменатель 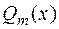на линейные и квадратные множители, для чего надо решить уравнение

.

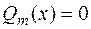
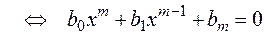Предположим, что это уравнение решено и найдены его корни. Согласно основной теореме алгебры, уравнение 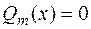имеет ровно 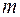корней с учетом их кратности. Корни уравнения могут быть действительными (простыми или кратными) и комплексными (простыми или кратными). Следовательно, разложение многочлена 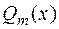на линейные и квадратные множители будет иметь вид:

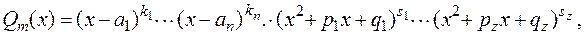где 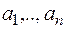― действительные корни многочлена кратности 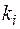, , 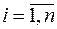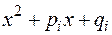― произведение комплексно сопряженных корней кратности 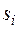(за пару) .

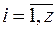Теорема. Правильную рациональную дробь 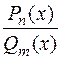, где 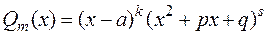, можно единственным образом разложить на сумму простейших дробей:

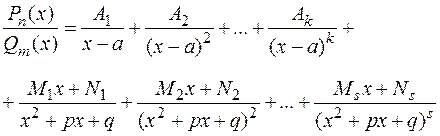(1)

где 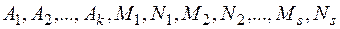— некоторые действи-тельные числа.

Согласно разложению (1), линейным множителям знаменателя 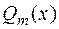соответствуют простейшие дроби первого и второго типов, а квадратным множителям — третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот мно­житель входит в разложение знаменателя дроби. Формула (1) разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя.

Проиллюстрируем формулу (1) конкретными примерами, не находя самих коэффициентов разложения:

,

.

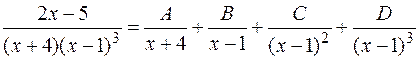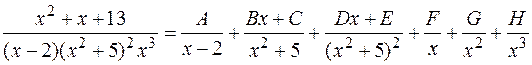Чтобы найти коэффициенты разложения, чаще всего при­меняют метод неопределенных коэффициентов и метод частных зна­чений.

Метод неопределенных коэффициентов. Суть метода неопреде­ленных коэффициентов состоит в следующем. Пусть дано разложе­ние правильной рациональной дроби 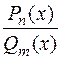по формуле (1) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю 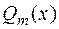и приравняем мно­гочлен, получившийся в числителе, многочлену .

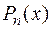Для тождественного равенства двух многочленов необходимо и достаточно, чтобы коэффициенты при одинаковых степенях 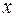этих многочленов были равны. Учитывая это, приравниваем коэффи­циенты при одинаковых степенях 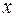в левой и правой частях получен­ного тождества. Имеем систему 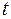линейных алгебраических урав­нений для нахождения 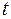неизвестных коэффициентов.

Пример. Разложить 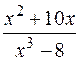на простейшие дроби.

Решение. Так как 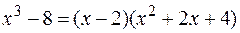, то

,

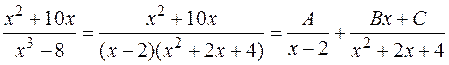где числа 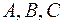пока неизвестны. Правую часть этого разложения приведем к общему знаменателю. Тогда

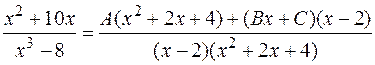
Следовательно,

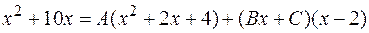
или

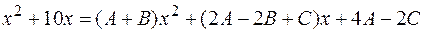
Приравнивая коэффициенты при одинаковых степенях 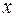, получаем систему урав­нений для нахождения неопределенных коэффициентов :

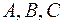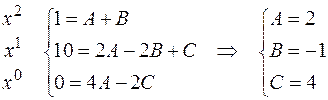
Таким образом,

.

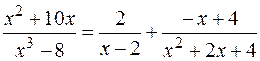Метод частных значений. При нахождении неопределенных коэф­фициентов вместо того, чтобы сравнивать коэффициенты при одина­ковых степенях 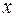, можно дать переменной 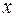несколько частных зна­чений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффи­циентов. Особенно выгодно применять этот метод в случае, когда корни знаменателя рациональной дроби 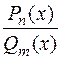просты и дейст­вительны. Тогда оказывается удобным последовательно полагать 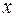равным каждому из корней знаменателя.

Пример. Разложить рациональную дробь 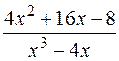на простейшие дроби.