Зависимость теплового эффекта от температуры. Уравнение Кирхгофа

Согласно закону Гесса можно вычислить тепловой эффект реакции при той температуре, при которой известны теплоты образования или теплоты сгорания всех реагентов (обычно это 298 К). Однако, часто возникает необходимость в том, чтобы знать тепловые эффекты реакций при различных температурах. Для вывода такой температурной зависимости воспользуемся уравнением

=

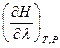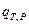
Если 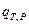- тепловой эффект химической реакции, протекающей до конца (D 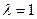), пр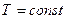и и 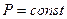, то тогда 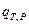просто равен ΔН реакции:

ΔН = Н₂ – Н₁ =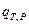

Здесь и в дальнейшем индекс «2» отнесён к продуктам реакции, а индекс «1» - к исходным веществам.

Запишем уравнение химической реакции в общем виде:

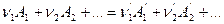
Через H_i обозначим энтальпию i -ого реагента, отнесённую к 1 моль вещества. Так как в результате одного пробега реакции исчезает 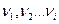моль исходных веществ и появляется 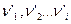моль продуктов реакции, то общее изменение энтальпии в процессе будет:

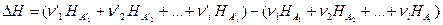
Продифференцируем это уравнение по температуре при

P=const: 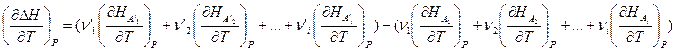Если теперь ввести обозначения:

=

=

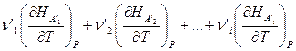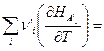
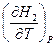
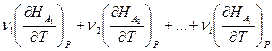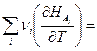
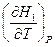
и принять во внимание, что 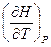есть истинная теплоёмкость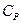

(смотри (I,58б)), то тогда

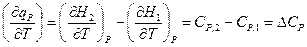
где 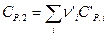и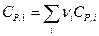

Или окончательно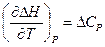

Как для идеальной системы, так и для реальных систем при невысоких давлениях частную производную от теплового эффекта по температуре можно заменить полной производной:

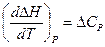(I, 67)

Это уравнение впервые было выведено Кирхгофом и называется его именем.

Интегрирование уравнения (I, 67) дает следующее выражение:

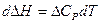
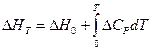(I, 67а)

Где 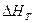- тепловой эффект реакции при заданной температуре, а 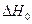- константа интегрирования, которую иногда ошибочно называют тепловым эффектом реакции при абсолютно нуле. 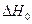имела бы этот смысл, если бы при интегрировании (I, 67) использовалась функция, сохраняющая своё значение до температур, близких к абсолютному нулю. В большинстве же практических случаев при интегрировании используются зависимости теплоёмкостей, действительные для относительно высоких температур и совершенно непригодные в области абсолютного нуля.

В первом приближении можно считать, что 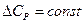, тогда интегрирование

(I, 67а) дает следующее выражение:

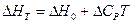
Если при интегрировании использовать температурную зависимость теплоемкостей в виде степенных рядов (смотри уравнение (I, 15)), то получим следующие более точные соотношения:

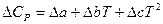
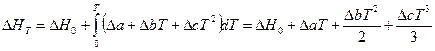(I, 67б),

где

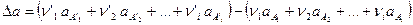
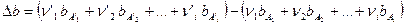
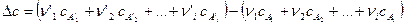
От трудностей, связанных с необходимостью вычисления константы интегрирования 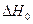, легко избавиться, если уравнение Кирхгофа проинтегрировать в интервале температур 298 ÷ Т:

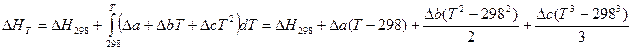
Тепловой эффект реакции при 298 К 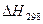может быть рассчитан с использованием четвертого или пятого следствий из закона Гесса.

Расчет тепловых эффектов по уравнению Кирхгофа с использованием температурных рядов для теплоемкостей является относительно трудоемким. Вычисления значительно упрощаются, если использовать значения средних теплоемкостей реагентов.

Если принять во внимание уравнение (I, 19), то можно записать:

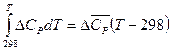, тогда

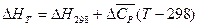(I, 68)