Согласно квантовой гипотезе Планка-Эйнштейна свет частотой n испускается, распространяется и поглощается веществом отдельными порциями (квантами), энергия которых e о= hn (h – постоянная Планка). Эти локализованные в пространстве дискретные световые кванты, движущиеся со скоростью с распространения света в вакууме, получили название фотонов. Таким образом, распространение света можно рассматривать не как непрерывный волновой процесс, а как поток частиц – фотонов. Доказательством этих квантовых (корпускулярных) представлений о свете, как о потоке частиц, являются фотоэффект и эффект Комптона.
Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения. Явление внешнего фотоэффекта и его закономерности объяснены на основе квантовой теории фотоэффекта, согласно которой каждый квант света поглощается только одним электроном.
Энергия hn падающего на металл фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии, то есть по закону сохранения энергии:
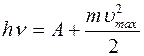 (уравнение Эйнштейна для внешнего фотоэффекта).
(уравнение Эйнштейна для внешнего фотоэффекта).
Из этого уравнения следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности, то есть от числа фотонов. Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается, то при некоторой частоте n = n 0 кинетическая энергия фотоэлектронов станет равной нулю и в том случае энергия фотона hn 0 равна работе выхода А, из чего следует, что n 0= А / h (частота n 0 носит название красной границы фотоэффекта). При частоте n<n 0 фотоэффекта не будет.
Масса и импульс фотона. Согласно квантовой гипотезе Планка-Эйнштейна, распространение света можно рассматривать как поток часииц – фотонов, энергия которых e 0 =hn. Тогда из уравнения Эйнштейна взаимосвязи массы и энергии E=mc2 следует, что масса фотона:
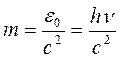 .
.
Фотон движется со скоростью света с, поэтому импульс р фотона:
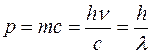 .
.
Полученные выражения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой характеристикой света – его частотой n (или его длиной волны l).
Корпускулярные свойства света проявляются в эффекте Комптона.
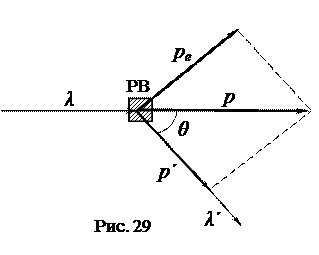
Эффектом Комптона называется увеличение длины волны коротковолнового электромагнитного излучения при его упругом рассеянии на свободных электронах вещества. Опыты Комптона показали, что разность длин волн рассеянного (l') и падающего (l) электромагнитного излучения, то есть величина Dl=l'–l не зависит от длины волны l падающего излучения и природы рассеивающего вещества (РВ), а определяется только углом рассеяния q, то есть углом между направлениями лучей до и после рассеяния (рис. 29):
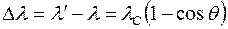 , где
, где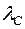 –комптоновская длина волны.
–комптоновская длина волны.
 Эффект Комптона не укладывается в рамки волновой теории света, и его объяснение дано на основе квантовых представлений о природе света. Если рассматривать излучение, как поток фотонов, то эффект Комптона – это результат упругого столкновения рентгеновских фотонов со свободными электронами рассеивающего вещества. В процессе этого столкновения фотон передает электрону часть своей энергии, что ведет к увеличению длины волны при рассеянии фотона.
Эффект Комптона не укладывается в рамки волновой теории света, и его объяснение дано на основе квантовых представлений о природе света. Если рассматривать излучение, как поток фотонов, то эффект Комптона – это результат упругого столкновения рентгеновских фотонов со свободными электронами рассеивающего вещества. В процессе этого столкновения фотон передает электрону часть своей энергии, что ведет к увеличению длины волны при рассеянии фотона.
(На рисунке 29 введены следующие обозначения: p и p' – импульсы фотона до и после рассеяния; pe – импульс электрона после рассеяния на нем фотона).
Исходя из законов сохранения импульса и энергии
|
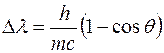 , где
, где 
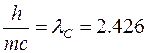 пм.
пм. 
Это выражение для величины D l, полученное на основе корпускулярных представлений о свете, оказалось аналогично приведенному выше выражению для величины D l, полученному Комптоном экспериментально.
Следовательно, эффект Комптона является экспериментальным доказательст-вом проявления корпускулярных свойств света как потока частиц – фотонов. Итак, рассмотренные явления фотоэффекта и эффекта Комптона служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов, а, с другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую природу света. Таким образом, свет, обладая одновременно корпускулярными и волновыми свойствами, проявляет так называемый корпускулярно-волновой дуализм.
Тема 14. Тепловое излучение
Излучение света телами, обусловленное их нагреванием, называется тепловым излучением. Количественно тепловое излучение характеризуется спектраль-ной плотностью энергетической светимости тела, т.е. мощностью излучения с единицы площади поверхности тела в интервале частот единичной ширины:
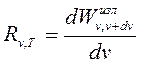 , где
, где
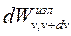 – энергия излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от n до n + dn.
– энергия излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от n до n + dn.
Спектральную плотность энергетической светимости можно представить в виде функции длины волны l, то есть в виде Rl,T, причем:
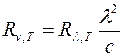 .
.
С помощью этой формулы можно перейти от Rn,T к Rl,T и наоборот.
Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимость RT:
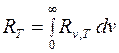 .
.
Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью Аn,T:
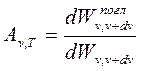 ,
,
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от n до n + dn, поглощается телом.
Тело, способное поглощать полностью при любой температуре всё падающее на него излучение любой частоты, называется черным телом. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице (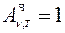 ).
).
Закон Кирхгофа. Кирхгоф установил, что отношение спектральной плотности энергетической светимости Rn,T к спектральной поглощательной способности Аn,T не зависит от природы тела; оно является для всех тел универсальной функцией rn,T частоты n (или длины волны l) и температуры Т:
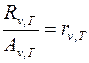 .
.
Для черного тела 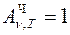 , поэтому из закона Кирхгофа вытекает, что универсальная функция Кирхгофа rn,T – это спектральная плотность энергетической светимости Rn,T черного тела. Тогда выражение для интегральной энергетической светимости черного тела Re можно записать в виде:
, поэтому из закона Кирхгофа вытекает, что универсальная функция Кирхгофа rn,T – это спектральная плотность энергетической светимости Rn,T черного тела. Тогда выражение для интегральной энергетической светимости черного тела Re можно записать в виде:
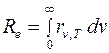 .
.
Энергетическая светимость черного тела Re зависит только от температуры.
Закон Стефана – Больцмана. Согласно закону Стефана – Больцмана энергетическая светимость черного тела Re зависит от температуры Т следующим образом: 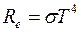 , где s – постоянная Стефана – Больцмана.
, где s – постоянная Стефана – Больцмана.
|
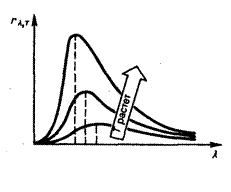 Закон смещения Вина. Из экспериментальных кривых зависимости функции rl,T от длины волны l при различных температурах (рис. 30) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют ярко выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн.
Закон смещения Вина. Из экспериментальных кривых зависимости функции rl,T от длины волны l при различных температурах (рис. 30) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют ярко выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Согласно закону смещения Вина, зависимость длины волны lmax, соответствующей максимуму функции rl,T, от температуры имеет вид: 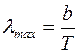 , где b – постоянная Вина.
, где b – постоянная Вина.
Это выражение называют законом смещения Вина, так как оно показывает смещение положения максимума функции rl,T с изменением температуры Т.
 2014-02-02
2014-02-02 8629
8629
