Преобразование Лапласа

Для решения обыкновенных дифференциальных уравнений в теории автоматического регулирования обычно используются преобразования Лапласа.

Преобразованием Лапласа называется соотношение

ставящее функции вещественного переменного y( 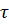) в соответствие функцию Y(p) комплексного переменного p = а +i 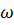. Функцию веще­ственного переменного y( 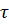) называют оригиналом, а функцию комплексного переменного Y(p) называют изображением по Лапла­су. Преобразование, выполненное в соответствии с выражением (8.33), называют прямым преобразованием и используют символическую за­пись Y(p) = L{y( )}.

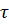Для нахождения оригинала по известному изображению применя­ется операция обратного преобразования Лапласа по соотношению

Часто используется символическая запись y( 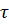) = L ^-1 {Y(p)}. Решение обыкновенных дифференциальных уравнений с исполь­зованием преобразования Лапласа производится в три этапа:

К дифференциальному уравнению применяется операция прямо­го преобразования.

Находится решение уравнения в операторной форме.

К решению уравнения в операторной форме применяется опера­ция обратного преобразования и находится оригинал функции.

Выполнение этих операций значительно упрощается, если приме­нить основные свойства преобразования Лапласа:

1. Свойство линейности - изображение суммы слагаемых равно
сумме изображений слагаемых, и константы можно выносить за знак
преобразования:

2. Дифференцирование оригинала при нулевых начальных условиях:

3. Интегрирование оригинала:

4. Теорема запаздывания:

5. Теоремы о предельных значениях:

6. Теорема разложения:

Если дробно-рациональная функция и степень полинома числителя меньше степени полинома зна­менателя, то оригинал можно получить, используя выражения: а) если все корни характеристического уравнения простые:

где p _к - простые корни уравнения

б) если все корни характеристического уравнения простые, а один корень нулевой:

где p1=0; остальные корни уравнения A(p) = 0 простые.

На основании основных свойств преобразований. Для упрощекния записи уравнения динамики операцию дифференцирования обозначают символом Р (здесь р-алгебраическая величина)

; ; …………

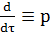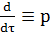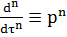
Аналогичны операции интегрирование обозначают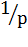

;

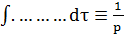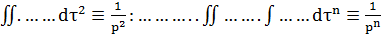
Таким образом

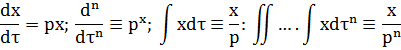
Используя эти соотношения, получим следующую запись уравнения динамики систем(1.6)

(a_n pⁿ+a_n-1p^n-1+….a_n-1p+a₀)y=(bmp^m+bm+p^m-1+….b_m-1p+b₀)x

Заменяя в левой части уравнения через D(p) на правой части через K(p), окончательно получим

D(p)y=K(p)x

Где D(p)-полином, характеризующее свободное. K(p) –полином, характеризующее внешнее возмущение. Уравнение динамики системы в операторной форме всегда, проще исходного дифференциальной уравнение. При этом оно учитывает начальные условия отражённая. Величину картину в переходном процессе в системе. Оригиналы обозначают строчными буквами с изображениями.

Таблица соответствия. Так как операция обратного преобразова­ния Лапласа (8.34) для многих функций является сложной математиче­ской задачей, то составлена таблица соответствия, в которой приведены оригиналы и соответствующие им изображения.

Ниже приведены несколько примеров.

Таблица 8.1

При отсутствии табличного соответствия необходимо предварительные их формы, для последующего нахождения оригинала.