Журнал измерения углов и длин сторон теодолитного хода

Дата: 15. 05.13 Теодолит 2Т30 №842

Наблюдал: И.П. Иванов Рулетка 30 – метровая

Записывал: П.П. Николаев Погода: Облачно, видимость хорошая.

Температура: +19º

Номер точки	Отсчет по горизонтальному кругу	Значение угла из полуприемов	Среднее значение угла	Длина линии, м (прямо, обратно, среднее)	Углы наклона ν	Горизонтальное проложение, м
стояния	визирования
		Л 246º 36,7' 61º 13,2' П 8º 23,6' 182º 59,1'	185º 23,5' 185º 24,5'	185º 24,0'	12 – 13 128,43 128,47 128,45	2º 30'	128,33
		Л 143º 18,0' 41º 02,0' П 320º 49,2' 218º 83,0'	102º 16,0' 102º 16,2'	102º 16,1'	13 – 14 215,28 215,19 215,24	1º 30'	215,15

Стороны теодолитных ходов измеряют рулетками или другими приборами, обеспечивающими требуемую относительную погрешность измерений 1/1000 – 1/3000. Рулетками стороны хода измеряют в прямом и обратном направлениях.

Теодолитом измеряют углы наклона. Поправки за наклон вводят при углах наклона, превышающих 1º.

Привязка теодолитного хода к исходным пунктам. Чтобы определить дирекционные углы сторон теодолитного хода и координаты его пунктов в государственной системе координат, выполняют привязку теодолитного хода к существующим пунктам геодезической сети, координаты которых известны. Чаще всего привязку выполняют непосредственным примыканием теодолитного хода к исходным пунктам. При таком примыкании на исходном опорном пункте А (рис.2) измеряют примычный угол ß между направлениями на другой опорный пункт С и на ближайшую точку теодолитного хода 1, а также длину стороны А1. Зная примычный угол ß, можно от дирекционного угла направления СА перейти к дирекционному углу первой стороны хода А - 1 и, зная координаты пункта А и длину стороны А - 1, вычислить координаты точки 1.

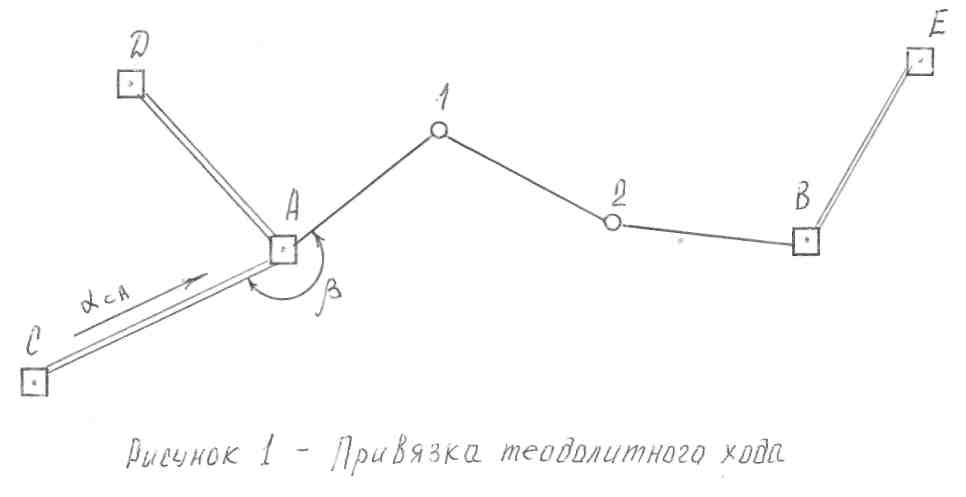
Рисунок 2 – Привязка теодолитного хода

При значительном удалении (более 5 км) участка съемки от пунктов государственной геодезической сети и сетей сгущения теодолитные ходы прокладывают без привязки к опорным пунктам. Одному из пунктов сети присваивают условные значения координат, а для ориентирования сети определяют астрономический азимут одной – двух её линий. На участках до 5 км² съемочные сети разрешается ориентировать по магнитному азимуту.

Вычисление координат пунктов разомкнутого теодолитного хода. Исходными данными при обработке являются координаты пунктов на которые ход опирается - начального x_н, у_н и конечного х_к, у_к пунктов, а также дирекционные углы α_н и α_к соответствующих примычных сторон опорной сети. В теодолитном ходе, схема которого показана на рисунке 3, исходными служат координаты пунктов полигонометрии ПП48, ПП61 и дирекционные углы примычных направлений ПП49 – ПП48 и ПП61 – ПП63.

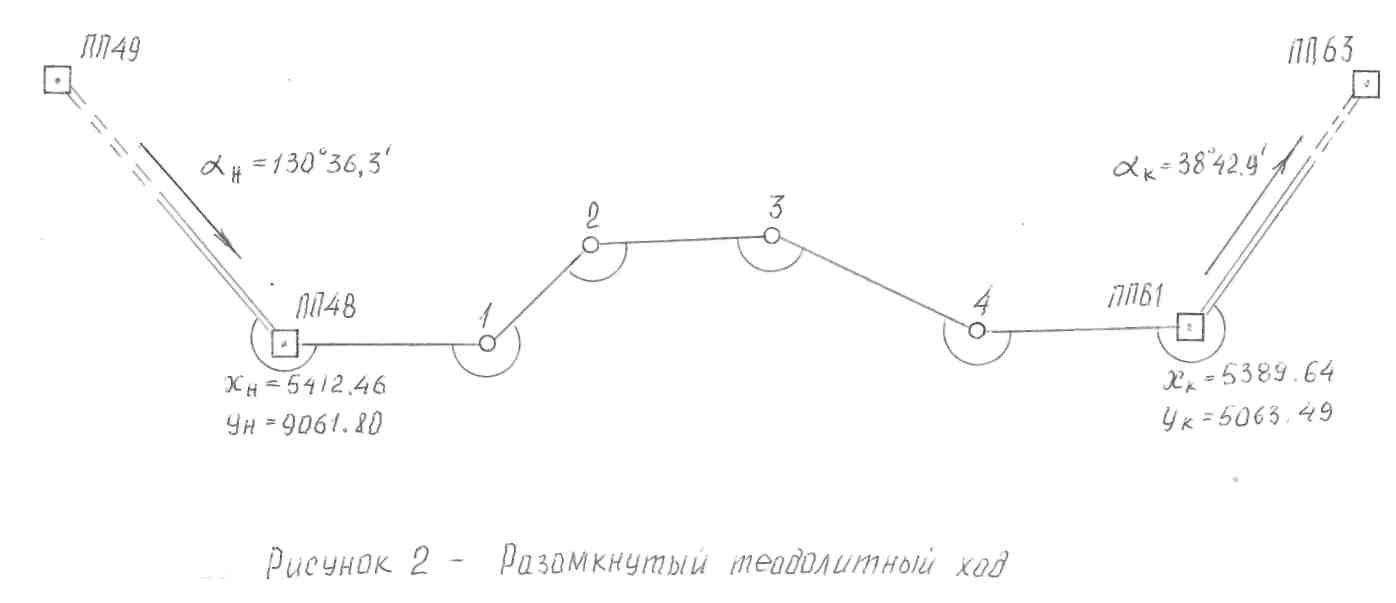
Рисунок 3 – Разомкнутый теодолитный ход

Записи в ходе вычислений ведут в координатной ведомости (табл.2). В графу 1 вписывают названия или номера пунктов в том порядке, как они расположены на схеме рис.3.

В графу 2 записывают измеренные на этих пунктах горизонтальные углы, а в графу 4 исходные начальный и конечный дирекционные углы (выделены подчерком). Координаты начального и конечного пунктов записывают в соответствующие строки граф 11 и 12 (тоже подчеркнуты), а в графу 6 горизонтальные проложения измеренных сторон хода.

Вычисляют сумму измеренных углов

∑ß_изм = ß₁+ ß₂+ ß₃+ ß₄.

Затем вычисляют теоретическое значение этой суммы по формулам:

для правых углов ∑ß_теор = α_н – α_к + n∙180º;

для левых углов ∑ß_теор = α_к – α_н + n∙180º.

Определяют угловую невязку хода

f_ß = ∑ß_изм - ∑ß_теор

и допустимую угловую невязку f_{ß доп} = 1'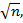

где n – число углов в ходе. Записи при вычислении невязок располагают внизу под таблицей.

Ведомость вычисления координат пунктов разомкнутого теодолитного хода

Таблица 2

Пункт

Углы (правые)

Дирекционный угол α

Румб

Горизонтальное проложение d, м

Приращения координат, м

Координаты, м

Пункт

Измеренный

Исправленный

Вычисленные

Исправленные

х

у

Δх

Δу

Δх

Δу

ПП49

130º 36,3´

-0,3´

ПП48

221º 16.4´

221º 16.1´

5412.36

3937.80

ПП48

-4

+9

89º 20.2´

246.13

+2.85

+246.11

+2.81

+246.20

-0.3

200º 52.1´

200º 51.8´

5415.17

4184.00

-5

+10

68º 28.4´

298.82

109.65

+277.98

+109.60

+278.08

-0.3

157º 28.5´

157º 28.2´

5524.77

4462.08

-4

+8

91º 00.2´

217.10

-3.80

+217.07

-3.84

+217.15

-0.3

143º 27.5´

143º 27.2´

5520.93

4679.23

-3

+7

127 º33.0´

197.91

-120.62

+156.91

-120.65

+156.98

-0.3

214º 52.8´

214º 52.8´

5400.28

4836.21

-4

+8

92 º40.2´

227.45

-10.60

+227.20

-10.64

+227.28

-0.4

ПП61

233º 57.7´

233º 57.3´

5389.64

5063.48

ПП61

38º 42.9´

ПП63

-22.72

1125.69

∑ß_изм = 1171º 55.3 ∑ß_теор = α_н – α_к + n∙180º = 1171º 53.4´

f_ß = ∑ß_изм - ∑ß_теор = 1.9´ f_{ß доп} = 1' 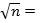2.4´

∑d = 1187.41; ∑Δх = - 22.52; ∑Δу = 1125.27;

х_к – х_н = - 22.72; у_к – у_н = 1125.69;

f_x = +0.20м; f_y = - 0.42м;

f = 0.46м;

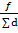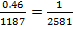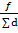= _{; ( )доп} =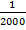

Если угловая невязка меньше допустимой, что указывает на доброкачественность выполненных угловых измерений и правильность вычислений, то невязку распределяют поровну на все измеренные углы. Поправки, равные невязке, взятой с обратным знаком и деленной на число углов, пишут над измеренными углами в графе 2, округляя до десятых долей минуты. Величину поправок контролируют суммированием и сравнением результата с невязкой.

Исправленные поправками углы вписывают в графу 3 и используют для вычисления дирекционных углов, которые записывают в графу 4.

Вычисление дирекционных углов ведут по формулам:

для правых углов

α_i+1 = α_i 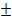180 – ß_i;

для левых углов

α_i+1 = α_i 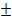180 + ß_i;

где α_i+1 – дирекционный угол следующей стороны; α_i – дирекционный угол предыдущей стороны; ß_i – угол между этими сторонами. Если угол α_i+1 оказывается больше 360º, то из него вычитают 360º.

В результате последовательного вычисления дирекционных углов всех сторон хода в конце должно быть получено значение дирекционного угла конечной стороны, равное заданному.

По дирекционным углам и горизонтальным проложениям вычисляют приращения координат

Δx_i = d_i cosα_i;

Δy_i = d_i sinα_i ,

которые, округлив до сотых долей метра, записывают в графы 7 и 8 ведомости.

Сложив вычисленные приращения координат, находят координатные невязки хода по формулам

f_x = ∑Δ_x – (x_к – х_н);

f_y = ∑Δ_y – (y_к - y_н),

где ∑Δ_x и ∑Δ_y – суммы приращений абсцисс и ординат.

Затем вычисляют линейную невязку

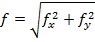
и относительную невязку хода

f / ∑d = 1/N,

где ∑d – длина хода, вычисленная суммированием его сторон.

Если относительная невязка f / ∑d меньше допустимой относительной невязки, равной 1/N = 1/2000, то невязки в координатах, взятые с обратными знаками, распределяют между вычисленными приращениями координат пропорционально горизонтальным проложениям соответствующих сторон хода. При этом поправки к приращениям координат, вычисленные по формулам

v _xi = - 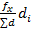; v _yi = -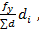

округляют до см и пишут над соответствующими приращениями координат.

Исправленные поправками приращения координат записывают в графы 9 и 10 ведомости и для контроля суммируют. Суммы должны равняться разностям исходных координат:

∑Δ_x = x_к – x_н; ∑Δ_y = y_к – y_н.

Вычисляют координаты пунктов хода. Начиная от начальной точки хода, прибавляют к координатам исправленные приращения координат и последовательно одну за другой вычисляют координаты всех точек:

x_i+1 = x_i + Δx_i; y_i+1 = y_i + Δy_i.

Контролем правильности вычислений служат совпадение вычисленных координат конечной точки хода с заданными.

Обработка замкнутого теодолитного хода. Исходными данными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. На рисунке 4 исходным пунктом является пункт полигонометрии ПП54, а исходным дирекционным углом – дирекционный угол направления из ПП54 на пункт 1,который вычисляют по примычному углу, измеренному на пункте ПП54 между направлениями на пункт 1 и на пункт ПП55, и известному дирекционному углу последнего направления.

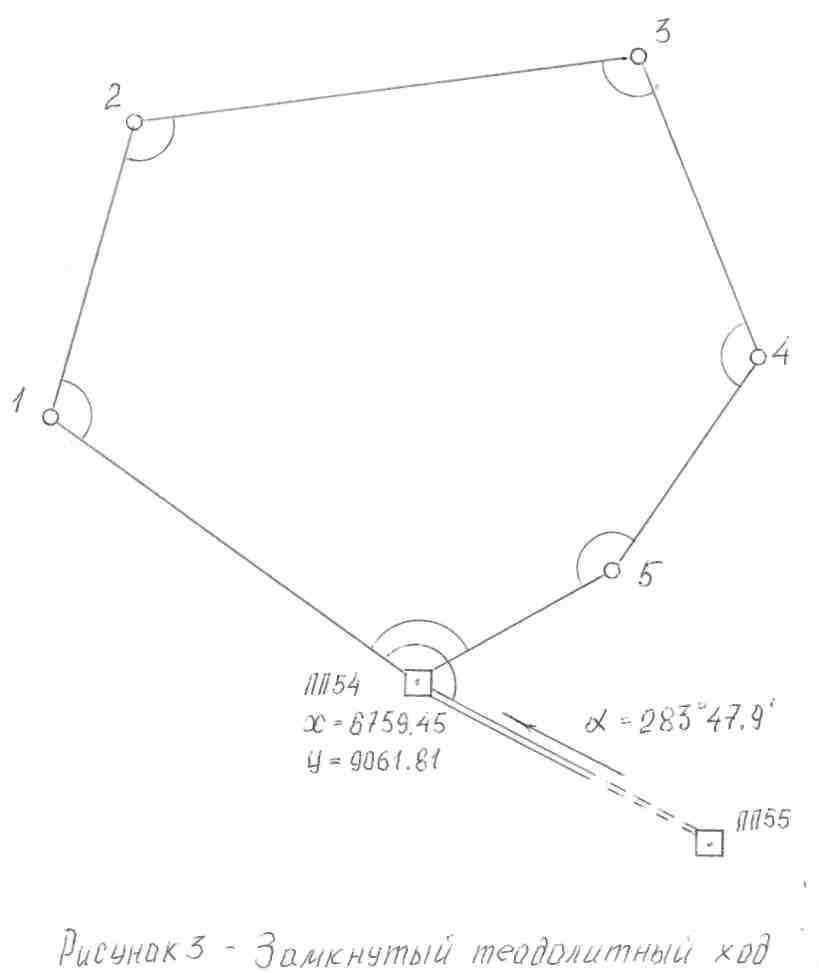
Рисунок 4 – Замкнутый теодолитный ход

В ведомость вычисления координат записывают в графы 1 и 13 номера пунктов, в графы 11 и 12 исходные координаты ПП54, в графу 2 – измеренные углы и в графу 6 – горизонтальные проложения. Используя примычный угол равный 164º 43,2´,вычисляют дирекционный угол стороны ПП54 – 1:

α_{пп54 – 1} = 283º 47.9´ + 180º – 164º 43.2´ = 299º 0.47´.

Определяют угловую невязку хода f_ß, пользуясь формулой

f_ß = ∑ß_изм - ∑ß_теор,

в которой

∑ß_теор = 180(n-2),

где n – число углов в полигоне. В нашем примере число углов в замкнутом полигоне равно 6, поэтому ∑ß_теор= 720º. Найденная невязка f_ß не должна превышать допустимой, вычисляемой по формуле

f_{ß доп} = 1'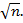

Распределяют невязку и вычисляют дирекционные углы так же, как в разомкнутом ходе. Контролем правильности вычислений служит получение в конце того же значения дирекционного угла, которое было исходным. Так в конце графы 4 ведомости для стороны ПП54 – 1 получено исходное значение 299º 04.7´.

Вычисление линейной и относительной невязок хода, распределение невязок в приращениях абсцисс и ординат и вычисление координат точек хода выполняется так же, как в случае разомкнутого хода. Контролем правильности вычислений служит получение для координат начальной точки хода в конце вычислений тех же координат, что были исходными. Так в конце графы 4 ведомости для стороны ПП54 – 1 получено исходное значение 299º 04.7´.

Вычислив приращения координат (графы 7 и 8), невязки в координатах находят по формулам

f_x = ∑Δ_x; f_y = ∑Δ_y.

Вычисление линейной и относительной невязок хода, распределение невязок в приращениях абсцисс и ординат и вычисление координат точек хода выполняется так же, как в случае разомкнутого хода. Контролем правильности вычислений служит получение для координат начальной точки хода в конце вычислений тех же координат, что были исходными.

Ведомость вычисления координат пунктов замкнутого теодолитного хода Таблица 3

Пункт	Углы (правые)	Дирекционный угол α	Румб	Горизонтальное проложение d, м	Приращения координат, м	Координаты, м	Пункт
Измеренный	Исправленный	Вычисленные	Исправленные	х	у
Δх	Δу	Δх	Δу
ПП55			283 47.9									ПП55
ПП54	164 43.2					+7	-3			6759.45	9061.81	ПП54
	- 0.4		299 04.7		173.11	+84.13	-151.29	+84.20	-151.32
	86 39.6	86 39.2				+10	-4			6843.65	8910.49
	-0.4		32 25.5		232.42	+196.18	+124.62	+196.28	+124.58
	127 13.9	127 13.5				+9	-4			7039.93	9035.07
	-0.4		85 12.0		212.22	+17.76	+211.48	+17.85	+211.44
	90 28.5	90 28.1				+8	-3			7057.78	9246.51
	-0.4		174 43.9		193.94	-193.12	+17.81	-193.04	+17.78
	128 46.2	128 45.8				+6	-3			6864.74	9264.29
	-0.3		225 58.1		144.72	-100.59	-104.05	-100.53	-104.08
	138 45.8					+4	-2			6764.21	9160.21
	-0.3		267 12.3		98.50	-4.80	-98.38	-4.76	-98.40
ПП54	148 07.9	148 07.6								6759.45	9061.81	ПП54
			299 04.7

∑ß = 720 02.2; ∑ß_теор = 720; ∑d = 1054.91; f_x = ∑Δ_x = - 0.44; f_y = ∑Δ_y = 0.19; f_ß = 2.2´; f_{ß доп} = 1' 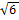= 2.4´; f = 0.48; f / ∑d = 1/2200; (f / ∑d)_доп = 1/2000.