Вычисление координат точек замкнутого теодолитного хода

Исходными данными для обработки замкнутого теодолитного хода являются координаты начальной точки X₁, Y₁ и дирекционный угол начальной линии хода α_1,2 (рисунок 11.1). Эти исходные данные определяются по результатам привязки теодолитного хода к пунктам государственной геодезической сети или выбираются независимо в условной системе координат.

В соответствии с исходными данными и результатами полевых измерений углов β и длин сторон d необходимо вычислить координаты других точек замкнутого теодолитного хода (2–6). Обработка результатов полевых измерений ведется в следующей последовательности:

1. Уравнивание углов замкнутого теодолитного хода.

Из геометрии известно, что сумма внутренних углов замкнутого многоугольника

Σβ_теор = 180^о(n – 2), (11.1)

где n – число вершин многоугольника.

Например, в шестиугольнике (n = 6)

Σβ_теор = 180^о(6 – 2) = 180^о? 4 = 720^о.

Эту сумму углов называют теоретической. Определяют практическую сумму измеренных горизонтальных углов хода и для контроля сравнивают ее с теоретической. Вследствие неизбежных погрешностей, которые возникают при измерении углов, сумма измеренных углов замкнутого теодолитного хода не будет точно равна теоретической.

Разность между практической и теоретической суммами углов называют угловой невязкой хода и обозначают f_β:

f_β = Σβ_пр – Σβ_теор. (11.2)

В теории погрешностей доказывается, что угловая невязка не должна быть больше предельной величины, которую называют допустимой невязкой, т. е.

f_{β доп} = ± 1,5t √ n, (11.3)

где t – точность отсчетного устройства теодолита;

n – число углов в теодолитном ходе.

Например, в теодолите Т-30 t = 1' и формула (11.3) примет вид

f_β_{доп =} ± 1,5' √ n. (11.4)

Для точных теодолитов (2Т5К, 3Т5К) допустимую угловую невязку вычисляют по более жесткой формуле

f_β _доп = 1' √ n. (11.5)

Невязка в углах может получиться недопустимой только в результате грубых просчетов при измерении углов или при вычислении их в журнале. Если невязка допустима, то ее распределяют с обратным знаком поровну на все углы теодолитного хода, т. е. вводят поправки в измеренные углы:

V_β = – (f_β / n). (11.6)

С учетом поправок вычисляют исправленные углы:

β_испр = β + V_β. (11.7)

Сумма исправленных углов должна быть равна теоретической сумме углов:

Σβ_испр = Σβ_теор. (11.8)

Эти действия по распределению невязки в углах, вычислению поправок и исправлению углов называются уравниванием углов теодолитного хода.

2 Вычисление дирекционных углов сторон замкнутого теодолитного хода.

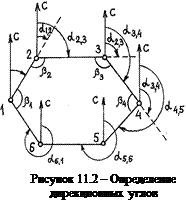
После уравнивания углов приступают к вычислению дирекционных углов сторон теодолитного хода. В замкнутом теодолитном ходе измеряют обычно внутренние углы β₁, β₂, β₃, …, β₆, лежащие вправо по ходу, их называют правыми углами (см. рисунок 11.1). Если начальный дирекционный угол α_1,2 из данных привязки неизвестен, то за него можно принять магнитный азимут, измеренный при помощи буссоли теодолита. Затем определяют дирекционные углы остальных линий теодолитного хода. Согласно рисунку 11.2

α_{2, 3} = α_{1, 2} + 180^о – β₂;

α_{3, 4} = α_{2, 3} + 180^о – β₃

и т. д., т. е. дирекционный угол последующей линии равен дирекционному углу предыдущей линии плюс 180^о, минус правый угол, лежащий между этими линиями:

α_посл = α_пред + 180^о – β_пр. (11.9)

Из рисунка 11.3 вытекает связь между левыми и правыми по ходу углами:

β_пр = 360^о – β_лев. (11.10)

Подставив (11.10) в формулу (11.9) получим:

α_посл= α_пред + 180^о – (360^о – β_лев)

или

α_посл= α_пред – 180^о + β_лев. (11.11)

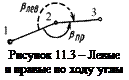
То есть по формуле (11.11) можно определить дирекционные углы, если известны левые по ходу углы β_лев. При получении по формулам (11.10) и (11.11) дирекционных углов больше 360^о из них вычитают 360^о.

Контролем правильности вычисления дирекционных углов в замкнутом теодолитном ходе является получение исходного (начального) дирекционного угла в конце вычислений (см. рисунок 11.2).

α_{1, 2}= α_{6, 1} + 180^о – β₁.

По вычисленным дирекционным углам определяют румбы сторон замкнутого теодолитного хода, используя формулы связи между дирекционными углами и румбами по четвертям.

3 Уравнивание приращений координат и вычисление координат замкнутого теодолитного хода.

Как известно из прямой геодезической задачи, приращения координат есть проекции стороны теодолитного хода на оси X и Y, которые определяются по формулам (рисунок 11.4):

(11.12)

ΔX = d cos α;

ΔY = d sin α.

Из аналитической геометрии известно, что сумма проекции сторон замкнутого многоугольника на его любую ось равна нулю, то есть можно записать:

ΣΔX_теор= 0;

ΣΔY_теор = 0.

Следовательно, для замкнутого теодолитного хода сумма всех приращений координат по осям ОХ и OY должна равняться нулю. Однако вследствие неизбежных погрешностей, которыми сопровождаются линейные и угловые измерения, практические суммы вычисленных приращений координат будут не равны нулю, т. е.

ΣΔX_пр = f_X;

ΣΔY_пр = f_Y.

Величины f_X и f_Y называются невязками в приращениях координат: f_X –по оси ОХ, а f_Y – по оси OY. Невязки f_X и f_Y являются следствием незамыкания теодолитного хода на величину 11' = f d, которую называют невязкой в периметре хода или линейной невязкой (рисунок 11.5).

Из прямоугольного треугольника 1,1', 1'' следует:

f_d =√ f_X² + f_Y ².

Относительная невязка не должна превышать в замкнутом ходе для благоприятной местности 1:2000, при неблагоприятных условиях измерений (высокая трава, пашня, пересеченная и холмистая территория) – 1:1000, которая, вычисляется по формуле

f_отн = f_d / Σd = 1 / (Σd / f_d),

где Σd – периметр хода, м.

Если это условие выполнено, невязки f_X и f_Y распределяют с обратным знаком на приращения координат пропорционально длинам сторон, вычисляя их по формулам

V_{X i} = – f_X?d_i / Σd; V_{Y i} = – f_Y d_i / Σd.

Значения поправок округляют до сантиметров. Контролем правильности вычисления поправок будет выполнение равенств

ΣV_{X I} = – f_X; ΣV_{Y I} = – f_Y

С учетом найденных поправок определяют исправленные приращения координат

ΔX_испр = ΔX + V_X; ΔY_испр = ΔY + V_Y.

Сумма исправленных приращений координат в замкнутом теодолитном ходе должна быть равна нулю, т. е.

ΣΔX_испр = 0; ΣΔY_испр = 0.

Эти действия по распределению невязок, вычислению поправок и исправленных приращений координат называют уравниванием приращений координат. По исправленным приращениям координат от точки с известными координатами последовательно вычисляют координаты вершин теодолитного хода, используя формулы прямой геодезической задачи:

(11.13)

X_посл = Х_пред + ΔХ_исп;