В разомкнутом теодолитном ходе

Камеральная обработка разомкнутого теодолитного хода проводится в той же последовательности, что и для замкнутого теодолитного хода, за исключением вычислений по определению теоретической суммы углов и теоретической суммы приращений координат в разомкнутом теодолитном ходе. Рассмотрим эти вопросы более подробно. Пусть между исходными сторонами CA и BD проложен разомкнутый теодолитный ход (рисунок 11.6) в котором измерены правые по ходу углы β₀, β₁, β₂, β₃, β_n и длины сторон d₁, d₂, d₃, d₄.

Рисунок 11.6 – Разомкнутый теодолитный ход

Обозначим дирекционные углы исходных сторон СА и BD соответственно α_нач и α_кон, тогда согласно рисунку 11.6 и формуле вычисления дирекционных углов (11.9) получим:

α_{А, 1} = α_нач + 180^о – β₀;

α_{1, 2} = α_{А, 1} + 180^о – β₁;

α_{2, 3} = α_{1, 2} + 180^о – β₂;

α_{3, В} = α_{2, 3} + 180^о – β₃;

α_кон = α_{3, В} + 180^о – β_n.

Cкладывая по столбцу данные равенства, будем иметь:

α_кон = α_нач + 180^оn – Σβ.

Тогда теоретическая сумма углов в разомкнутом теодолитном ходе

Σβ_теор = α_нач + 180^оn – α_кон.

Если сумму измеренных углов хода обозначить Σβ_пр., то угловую невязку в разомкнутом теодолитном ходе можно вычислить по формуле

f_β = Σβ_пр – Σβ_теор = Σβ_пр – (α_нач + 180^оn – α_кон).

Если эта невязка допустима, то ее распределяют с обратным знаком поровну на все углы с соответствующим округлением, то есть вычисляют поправку в углы по формуле (11.6). С учетом полученных поправок определяют исправленные углы по формуле (11.7) и проверяют выполнение контрольного равенства по формуле (11.8).

После уравнивания углов разомкнутого теодолитного хода приступают к вычислению дирекционных углов всех линий хода, которые выполняют по формуле (11.9). В конце этих вычислений необходимо точно получить дирекционный угол конечной стороны α_кон., что покажет правильность выполненного расчета.

Вычисление теоретической суммы приращений координат в разомкнутом теодолитном ходе. Разомкнутый теодолитный ход проложен между опорными точками А и В с известными координатами Х_А, Y_A и X_B, Y_B (см. рисунок 11.6).

На основании формулы вычисления координат точек (11.13) можно записать:

Х₁ = Х_А + ΔХ_{А, 1}; Y₁ = Y_A + ΔY_{A, 1};

Х₂ = Х₁ + ΔХ_{1, 2} ; Y₂ = Y₁ + ΔY_{1, 2};

Х₃ = Х₂ + ΔХ_{2, 3}; Y₃ = Y₂ + ΔY_{2, 3};

Х_В = Х₃ + ΔХ_{3, В}; Y_B = Y₃ + ΔY_{3, B}.

Cкладывая по столбцу левые и правые части равенств соответственно найдем, что теоретически

Х_В = Х_А + ΣΔХ;

Y_B = Y_A + ΣΔY,

откуда

ΣΔХ_теор= Х_В – Х_А;

ΣΔY_теор = Y_B – Y_A.

Однако ввиду неизбежных случайных погрешностей, которые возникают при угловых и линейных измерениях, практическая сумма приращений координат не будет точно равна теоретической сумме приращений координат. В результате этого получатся невязки в приращениях координат f_X и f_Y,:

f_X = ΣΔX_пр – ΣΔХ_теор = ΣΔХ_пр – (Х_В – Х_А);

f_Y = ΣΔY_пр – ΣΔY_теор = ΣΔY_пр – (Y_B – Y_A).

Определение линейной невязки в периметре разомкнутого теодолитного хода f_d и относительной невязки f_отн, а также уравнивание приращений координат и вычисление координат выполняются также, как и в замкнутом ходе. Контролем вычисления координат в разомкнутом теодолитном ходе будет получение в конце вычислений по формуле (11.13) координат конечной точки (Х_В и Y_B).

Все вычисления по обработке замкнутого и разомкнутого теодолитных ходов ведут по соответствующим графам специальной ведомости, образец которой приведен в методических указаниях для выполнения лабораторных и расчетно-графических работ.

Составление планов теодолитной съемки

Основными документами для составления планов теодолитной съемки являются журнал полевых измерений и абрис. Существует несколько способов построения планов теодолитной съемки.

1. Построение планов по измеренным углам и длинам сторон.

Для построения плана этим способом необходимо иметь все внутренние углы и длины сторон теодолитного хода, а также дирекционный угол исходной стороны.

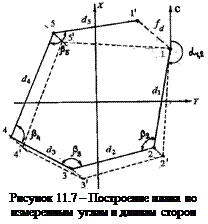
Посередине листа чертежной бумаги прочерчивают тонкую линию – направление меридиана (рисунок 11.7). Затем намечают первую точку замкнутого хода с таким расчетом, чтобы он разместился примерно в середине листа. После этого при помощи транспортира проводят из точки 1 линию 1 – 2 под заданным дирекционным углом и откладывают ее длину в масштабе плана. При точке 2 строят транспортиром угол β₂, вправо по ходу лежащий, и прочерчивают направление линии 2 – 3 и откладывают в масштабе длину этой линии, получая точку 3, и т. д.

В конечном результате, прочертив направление последней линии (на рисунке 11.7 это линия 5 – 1) и отложив ее длину, из-за неизбежных погрешностей, которые накапливаются при построении плана, полигон не замкнется. Величина отрезка 1 – 1' будет характеризовать невязку в периметре полигона. Эта невязка не должна превышать 1:200 периметра. Если невязка допустима, то полигон необходимо графически уравнять методом параллельных линий.

Для графического определения поправок прочерчивают прямую (рисунок 11.8), намечают на ней точку 1 и последовательно откладывают все линии полигона. Получают точки 1, 2, 3, 4, 5, 1'. В точке 1' строят перпендикуляр, откладывают на нем величину невязки 1' – 1 в масштабе плана и вершину его соединяют с точкой 1. Прочертив в точках 2, 3, 4, 5 перпендикуляры к прямой, получим отрезки V₂, V_3, V_4, V₅, являющиеся графическими поправками, на величину которых надо сместить соответствующие точки полигона. Затем прочерчиваем на плане через вершины 2, 3, 4, 5 короткие линии параллельные невязке в направлении 1' – 1 и откладываем отрезки V_2, V_3, V_4, V₅. Получаем исправленное положение точек 2', 3', 4', 5'. Соединив их между собой, получим уравненный полигон (на рисунке 11.7 он показан пунктирной линией).

Рисунок 11.8 – Графический способ определения поправок

2. Построение плана по дирекционым углам.

Этот способ несколько точнее предыдущего, так как здесь погрешности графического построения направления предыдущих линий не будут влиять на точность построения направлений последующих линий. Каждая линия в этом способе строится на плане по заранее вычисленным дирекционным углам или румбам. Внутренние углы используются здесь только для контроля в процессе работы.

Для построения плана берут лист чертежной бумаги, намечают первую точку хода и от направления меридиана откладывают дирекционный угол α_1,2 и по полученному направлению в масштабе плана откладывают длину линии 1 – 2 (рисунок 11.9). Затем при точке 2 проводят направление осевого меридиана, от которого откладывают дирекционный угол и длину линии 2 – 3 и т. д. В конце построения из-за неизбежных графических погрешностей получится невязка в периметре хода (величина 1 – 1'), которая не должна быть больше 1:300. Уравнивание невязки теодолитного хода производится также методом параллельных линий, как и в предыдущем способе.

Основным недостатком описанных способов составления планов является то, что погрешность нанесения предыдущей точки влияет на все последующие точки, т. е. получается накопление графических погрешностей. Поэтому рассмотрим способ, где каждая точка хода наносится на план независимо от других точек.

3. Составление плана по координатам.

Данный способ можно применять после вычисления координат точек теодолитного хода. Основным преимуществом его является то, что здесь нет возрастающего накопления погрешностей в положении точек.

Для удобства нанесения точек на план и для повышения точности его, на листе чертежной бумаги строят сетку квадратов, которая называется координатной сеткой. Построение сетки квадратов можно выполнять с помощью измерителя и масштабной линейки или с помощью линейки Дробышева.

Проводим на листе чертежной бумаги с его углов две диагонали (рисунок 11.10). Затем с помощью циркуля-измерителя откладываем из точки пересечения диагоналей (точка a) произвольные, но равные отрезки на диагоналях (ab, ac, ad, ae). Соединим концы отрезков и получаем прямоугольник, на сторонах которого откладываем равные отрезки по 10 или 5 см. Соединив соответствующие противоположные точки на сторонах прямоугольника получаем, сетку квадратов. В сетке квадратов проверяют равенство сторон квадратов и диагоналей в каждом квадрате. После построения и проверки сетки квадратов производят ее оцифровку, которую выполняют с таким расчетом, чтобы все точки хода разместить в пределах сетки квадратов.

На рисунке 11.11 показана роспись сетки квадратов для масштаба 1:2000 и нанесение на план точек 1 и 2. Точка 1 имеет координаты Х₁ = 0; Y₁ = 0, т. е. она лежит в начале координат. Для нанесения точки 2, координаты которой Х₂ = 632 м; Y₂ = 247 м, предварительно был определен квадрат, в котором она должна находиться, а затем согласно абсциссе точки 2 по вертикальным сторонам квадрата отложены отрезки, равные 32 м. Полученные точки соединены горизонтальной прямой, на которой от координатной линии 200 м отложен отрезок 47 м. Нанесение точек контролируется измерением расстояния между двумя соседними точками. Расхождение в расстояниях с данными ведомости координат не должно превышать 0,2–0,3 мм.

После нанесения точек теодолитных ходов на план приступают к нанесению ситуации местности в строгом соответствии с данными абриса. При этом процесс и способы построения точек ситуации на плане будут аналогичны соответствующим полевым действиям при съемке этих точек на местности, с той только разницей, что при построении плана роль землемерной ленты выполняет измеритель с масштабной линейкой, роль теодолита – транспортир, а роль экера – прямоугольный треугольник. Обычно вначале строят ситуацию, заснятую по сторонам основного замкнутого хода, а затем – по сторонам внутреннего разомкнутого хода. После нанесения ситуации план оформляют в соответствии с общепринятыми условными знаками.