Задания для самостоятельного решения

Построить графики амплитудно-фазовой, вещественной и мнимой частотных характеристик для передаточных функций при следующих значениях параметров:

К=5; Т₁=0,7; Т₂=0,2; Т₃=0,05; Т₄=0,01; λ=0,8.

1.

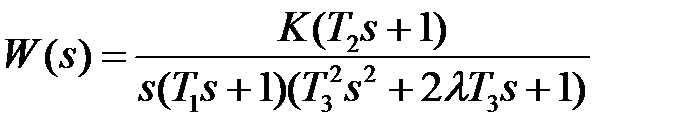
2.

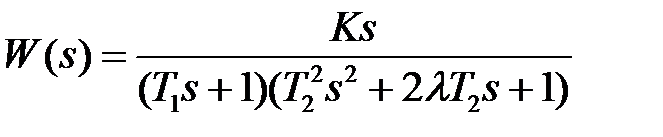
3.

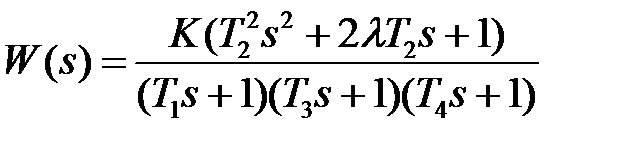
4.

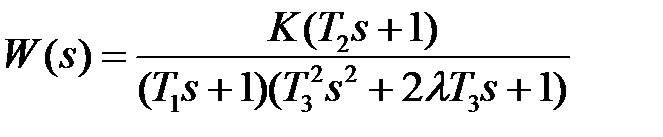
5.

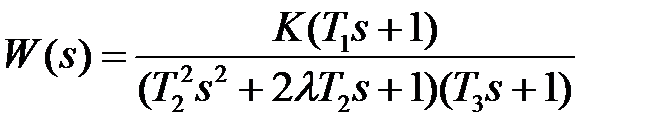
6.

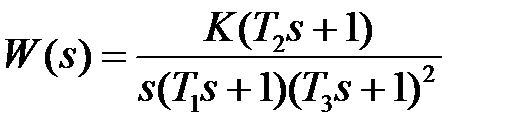
7.

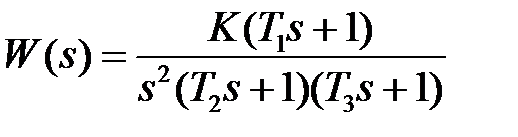
8.

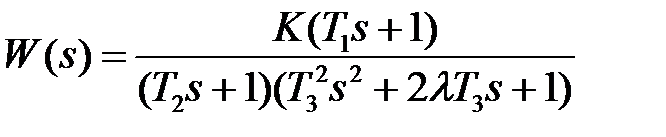
9.

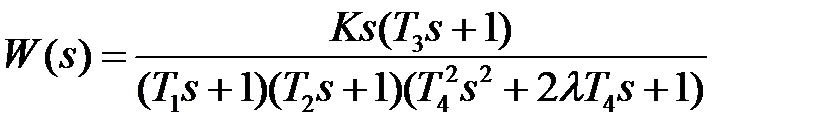
10.

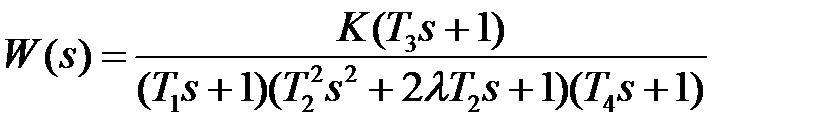
Построение логарифмических частотных характе­ристик.

Для построения логарифмической амплитудной (ЛАЧХ) и фазовой (ЛФЧХ) частотной характеристик звена с произвольной дробно-рациональной передаточной функцией W(s) нужно ее чис­литель и знаменатель разложить на элементарные множители и представить W(s) в виде произведения передаточных функций эле­ментарных звеньев:

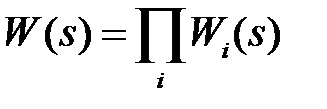(1)

или в виде

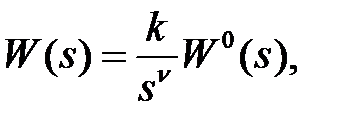(2)

где 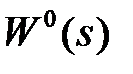представляет собой отношение произведений элементарных множителей 1-го и 2-го порядков с единичным передаточным коэффициентом, т.е. множителей вида Ts ± 1 и as² ± bs + 1 (b² — 4а < 0).

Из (2) получаем

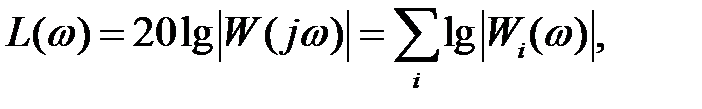(3)

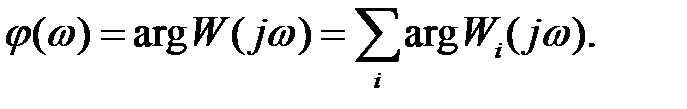
Из (3) следует, что для построения ЛАЧХ произвольного звена достаточно построить ЛАЧХ элементарных звеньев, на которые она разлагается, а затем их геометрически сложить. Однако для пост­роения асимптотических ЛАЧХ можно использовать несколько иное, более простое правило. Проиллюстрируем это сначала на частном примере.

Пусть 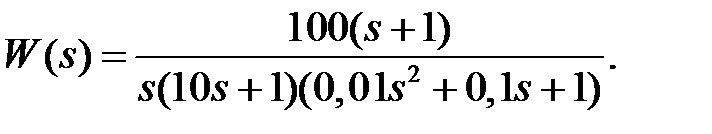Логарифмическая амплитудная частотная функция имеет вид

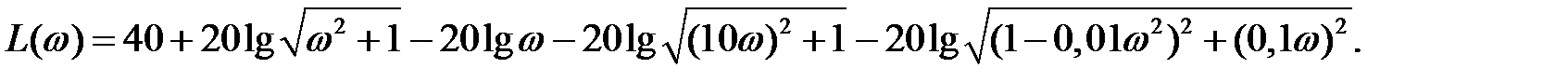Вычислим сопрягающие частоты и пронумеруем их в порядке воз­растания:

ω ₁ = 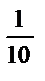= 0,1, ω₂ = 1, ω ₃ = 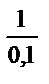= 10.

Здесь ω₁, ω₂ и ω₃ — сопрягающие частоты апериодического, форси­рующего и колебательного звеньев соответственно.

Напомним, что при построении асимптотических ЛАЧХ при час­тотах, меньших сопрягающей частоты, под корнем оставляют только единицу (остальными членами пренебрегают); при частотах, боль­ших сопрягающей частоты, оставляют член с наивысшей степенью ω. Поэтому в рассматриваемом примере при ω < ω₁

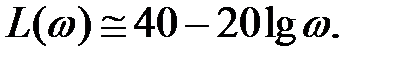
Это уравнение прямой, которая проходит через точку с координа­тами ω = 1 и L = 40 с наклоном —20 дБ/дек. Прямая имеет нак­лон —20дБ/дек (20дБ/дек); это означает, что при увеличении час­тоты на декаду (т.е. в 10 раз) L(ω) уменьшается (увеличивается) на 20 дБ (рис. 1 a).

Первая асимптота заканчивается на первой сопрягающей частоте (рис. 1 б).

При ω ₁ ≤ ω≤ ω ₂ аналогично имеем

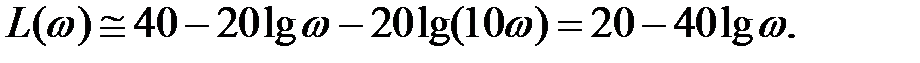
Это уравнение второй асимптоты. Ее наклон по отношению к первой асимптоте изменяется на - 20 дБ/дек и обуславливается апериодичес­ким звеном, т.е. множителем 1-го порядка в знаменателе рассматри­ваемой передаточной функции. Вторую асимптоту проводят от конца первой асимптоты до второй сопрягающей частоты согласно ее урав­нению под наклоном - 40 дБ/дек.

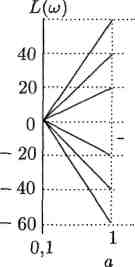
а б

Рис. 1.

При ω₂ <ω<ω₃

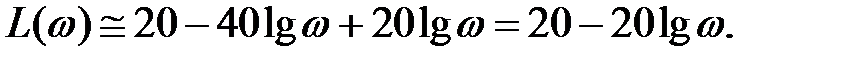
Это уравнение третьей асимптоты. Ее наклон по отношению ко вто­рой асимптоте изменяется на 20 дБ/дек и обуславливается форсирую­щим звеном, т. е. множителем 1-го порядка в числителе. Третью асимптоту проводят от конца второй асимптоты до третьей сопря­гающей частоты под наклоном - 20 дБ/дек.

При ω>ω₃

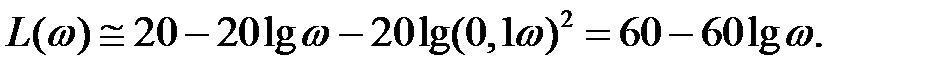
Это уравнение последней, четвертой асимптоты. Ее наклон изменяет­ся по отношению к третьей асимптоте на - 40 дБ/дек и обуславлива­ется колебательным звеном, т. е. множителем 2-го порядка в знамена­теле.

Теперь нетрудно сформулировать правило построения асимп­тотических ЛАЧХ в общем случае.

Правило построения асимптотических ЛАЧХ.

1) Пользуясь представлением (рис. 1.), вычислить 20lg(k)и сопряженные частоты ω_i = 1/T_i, которые следует пронумеровать в порядке возрастания: ω ₁ < ω₂ <…

2) На оси абсцисс отметить сопрягающие частоты, а на координат­ной плоскости — точку (1, 20lg(k)). Построить первую асимптоту — прямую под наклоном - v20 дБ/дек, проходящую через отмеченную точку на координатной плоскости. Первая асимптота заканчивается на первой сопрягающей частоте ω ₁.

3) Построить вторую асимптоту, которая начинается с конца пер­вой асимптоты и проводится до второй сопрягающей частоты ω ₂. Её наклон изменяется на ±20 дБ/дек или ±40 дБ/дек в зависимости от того, обуславливается ω ₁ элементарным множителем 1-го или 2-го по­рядка. Берется знак плюс, если указанный множитель нахо­дится в числителе, и знак минус, если этот множитель находится в знаменателе.

4) Построить остальные асимптоты, которые строятся аналогич­но второй асимптоте: i-я асимптота начинается с конца предыдущей, (i- 1)-й асимптоты и проводится до сопрягающей частоты ω_i. Его наклон определяется сопрягающей частотой ω_i -1.

5) Последняя асимптота представляет прямую, которая начинается с конца асимптоты, закачивающейся на последней сопрягающей часто­те, и уходит в бесконечность.

6)Примечание. Асимптотическая ЛАЧХ наиболее сильно отли­чается от точной ЛАЧХ в точках излома (при сопрягающих часто­тах). Причем в точках излома, где наклон изменяется на ±20 дБ/дек, это отличие (при условии, что соседние точки излома располагают­ся не очень близко) примерно равно ЗдБ/дек. В точках излома, где наклон изменяется на ±40дБ/дек, т.е. при сопрягающих частотах, обуславливаемых форсирующим звеном 2-го порядка или колебатель­ным звеном, отклонение зависит от коэффициента ζ и при малых ζ может быть значительным.

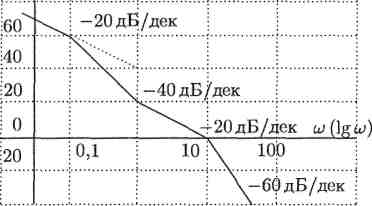
Пример 1. Построить асимптотическую ЛАЧХ звена с переда­точной функцией

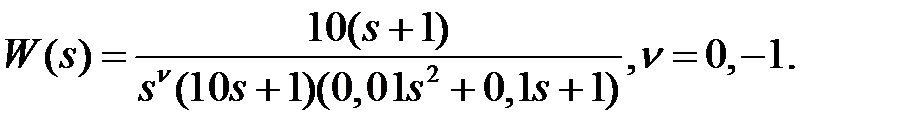
Решение. 1) v = 0. Вычислим 20lg(k) и сопрягающие частоты:

201gk = 201gl0 = 20;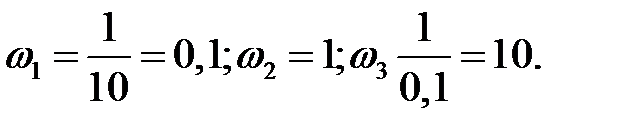

Проводим через точку с координатами (1, 20) первую асимпто­ту под наклоном 0дБ/дек (т.е. параллельно оси абсцисс) до первой сопрягающей частоты ω ₁= 0,1 (рис. 2 а).

Так как первая сопрягающая частота ω ₁обусловлена множите­лем 1-го порядка (10s+1), расположенного в знаменателе, наклон второй асимптоты изменяется на - 20 дБ/дек.

а) б)

Рис. 2

Поэтому вторую симптоту проводим от конца первой асимптоты до сопрягающей частоты ω ₂= 1 под наклоном —20 дБ/дек.

Сопрягающая частота ω ₂обусловлена элементарным множите­лем (s+1), расположенным в числителе. Поэтому наклон третьей асимптоты отличается от наклона второй на 20 дБ/дек и состав­ляет 0 дБ/дек. Третью асимптоту проводим от конца второй асимп­тоты до сопрягающей частоты ω ₃= 10.

Сопрягающая частота ω ₃обусловлена элементарным множи­телем 0,01 s² + 0,1s + 1, расположенным в знаменателе. Поэтому наклон последней, четвертой асимптоты отличается от наклона третьей асимптоты на - 40 дБ /дек и составляет - 40 дБ/дек. Пос­леднюю асимптоту проводим от конца третьей асимптоты до бес­конечности.

2) v = -1. Значения 20lg(k); и сопрягающих частот те же, что и в предыдущем случае. Первую асимптоту проводим через точку с ко­ординатами (1, 20) под наклоном - v 20 дБ/дек = 20 дБ/дек до первой сопрягающей частоты (рис. 2 б). Все последующие асимптоты стро­ятся так же, как и в предыдущем случае.

Пример 2. Построить ЛАХ и ФЧХ для передаточной функции

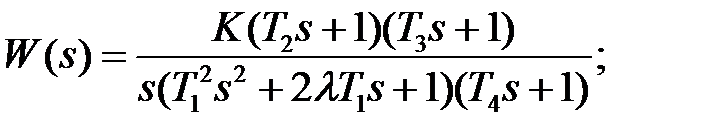
K= 10; Т ₁ = 0,5; Т ₂ = 0,1; Т ₃ = 0,05; Т ₄ = 0,01; λ= 0,8.

Решение:

1. Запишем выражение для амплитудно-фазовой характеристики

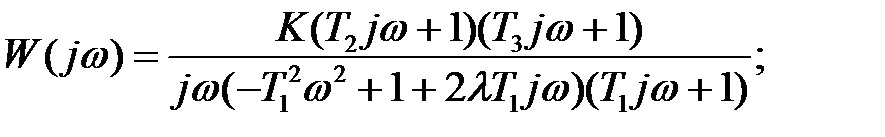
2. На основании полученного выражения, взяв модуль, получим амплитудно-частотную характеристику

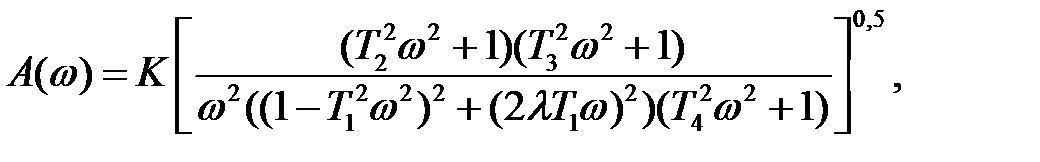и

логарифмическую амплитудную характеристику(ЛАХ).

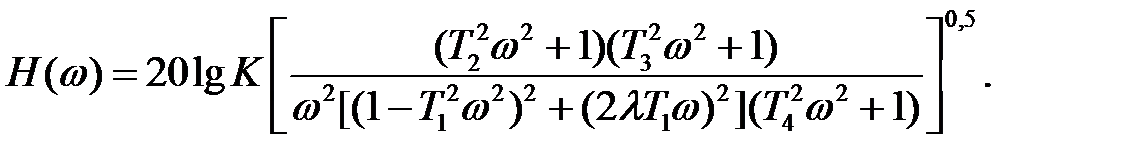
3. На основании того же выражения запишем функцию, описывающую фазо-частотную характеристику

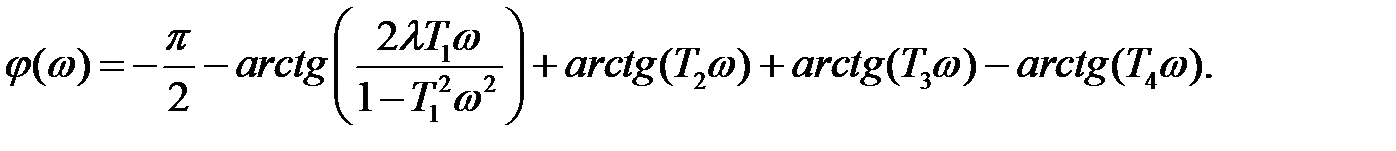
Для вычисления этих характеристик и для построения графиков воспользуемся средствами MatLab.

Ниже приведена программа MatLab и результаты ее выполнения с краткими комментариями.

>>k=10;, T1=0.5;, T2=0.1;, T3=0.05;, T4=0.01;, L=0.8; %Заносим значения параметров передаточной функции.

>> w=logspace(-2,3,100); % Задаём 100 значений частоты от 0,01 до 1000.

>> A=k*((T2^2*w.^2+1).*(T3^2*w.^2+1)).^0.5./...

>>(w.*((1-T^2.*w.^2).^2+2*L*T1*w.^2).^0.5.*(T4^2*w.^2+1).^0.5); %Вычисляем значения амплитудно-частотной характеристики в заданных точках.

>>plot(log10(w),20*log10(A)) %Строим график ЛАХ. (рис. 3.)

>> grid on %Наносим сетку

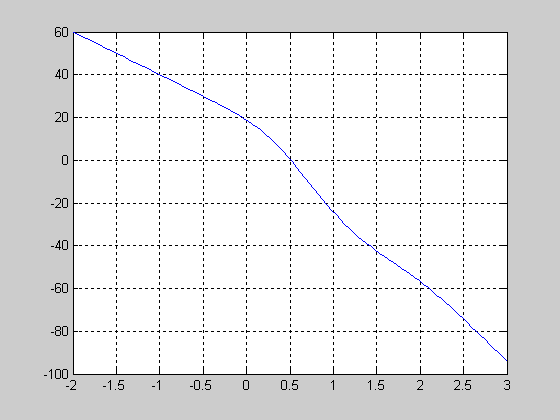
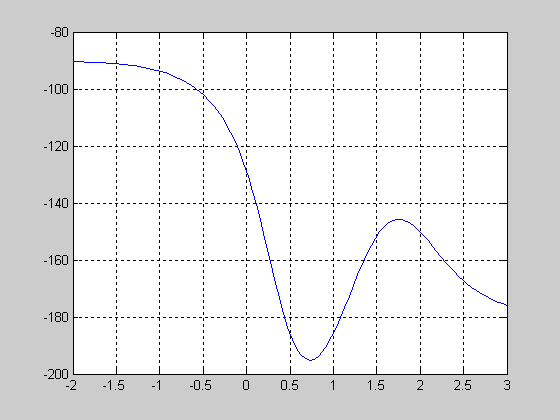
Рис. 3.

Рис. 4.

>>F=-pi/2-atan(2*L*T1*w./(1-T1.^2*w.^2))+atan(T2*w)+atan(T3*w)-… atan(T4*w); %Вычисляем значение фазо-частотной характеристики в заданных точках.

>> figure %Открываем еще одно графическое окно

>> plot(log10(w),F) %Строим график зависимости фазы от частоты, рис. 5.

>>f=0.5*unwrap(2*F); %Устраняем разрыв фазы.

>>plot(log10(w),f*360/(2*pi)) %Строим график зависимости фазы от частоты с устраненным разрывом фазы, рис. 4.

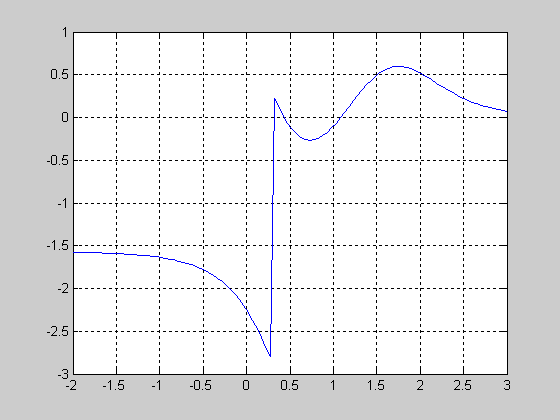
>> grid on %Наносим сетку

Рис. 5.