Изображение выходного сигнала системы управления X(s) может быть найдено как произведение изображения входного воздействия G(s) на передаточную функцию W(s)
X(s) = G(s)·W(s). (1)
Если на вход САУ подаётся единичное воздействие g(t)=1[t], то реакция системы на это воздействие называется переходной функцией и обозначается как h(t). Изображение выходного сигнала при этом будет:
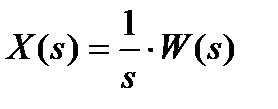 . (2)
. (2)
Следовательно, чтобы найти переходную функцию необходимо взять обратное преобразование Лапласа от входного сигнала.
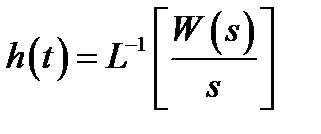 . (3)
. (3)
Импульсной функцией называется реакция системы на δ- воздействие. Учитывая, что изображение δ(t)-функции равно 1, импульсную функцию можно найти, как обратное преобразование Лапласа от передаточной функции системы
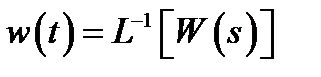 . (4)
. (4)
где 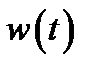 - импульсная функция системы.
- импульсная функция системы.
Оригинал 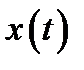 может быть найден в результате обратного преобразования Лапласа над его изображением
может быть найден в результате обратного преобразования Лапласа над его изображением
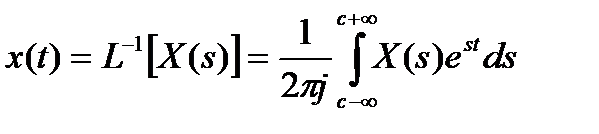 (5)
(5)
Вычисление оригинала может быть произведено с помощью вычетов по формуле
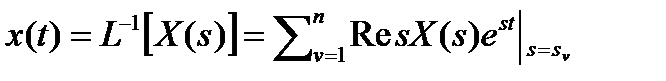 (6)
(6)
где 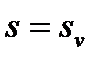 полюсы функции
полюсы функции 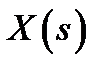 . При t< 0 следует положить
. При t< 0 следует положить 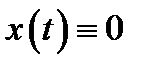
Рассмотрим случай, когда изображение 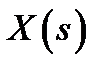 является дробно-рациональной функцией, т.е представляет собой отношение двух многочленов
является дробно-рациональной функцией, т.е представляет собой отношение двух многочленов
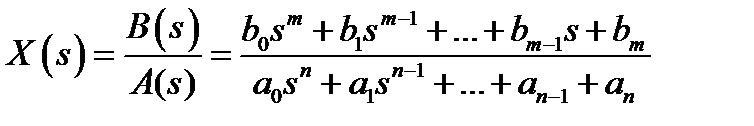 (7)
(7)
причём m<n и коэффициенты 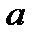 и
и 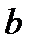 - действительные. Вычислив корни знаменателя
- действительные. Вычислив корни знаменателя 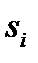
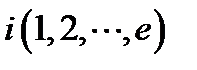 , представим это изображение в виде
, представим это изображение в виде
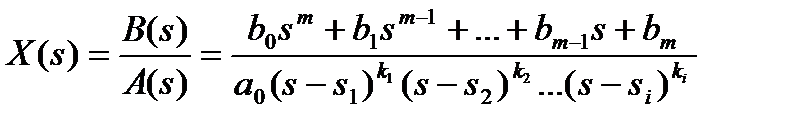 (8)
(8)
Здесь 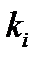 - кратность корня
- кратность корня 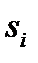 , причём
, причём 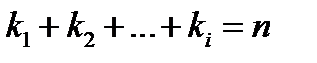
Нахождение вычета в полюсе 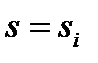 , кратности
, кратности 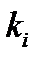 при t> 0 производится по формуле
при t> 0 производится по формуле
ResX(s)  est =
est = 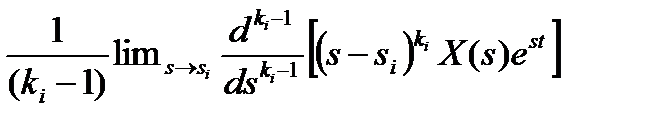 (9)
(9)
Пусть все корни знаменателя изображения X(s) простые, т.е ki(i= 1,2 ,…,n). Так как a 0 (si – s 1 ) (si – s2)… (si – s i-1 )…(si - sn)= 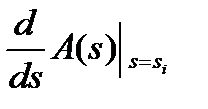 в этом случаи
в этом случаи 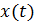 можно вычислить по формуле
можно вычислить по формуле
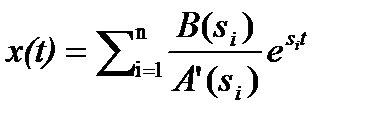 t>0.
t>0.
При наличии у многочлена A(s) пары мнимых корней s1=jω1, s2= ̶ jω1 имеем
A(s)=(s-jω1)(s+ jω1)A2(s)=(s2+ω12)A2(s).
x(t)= 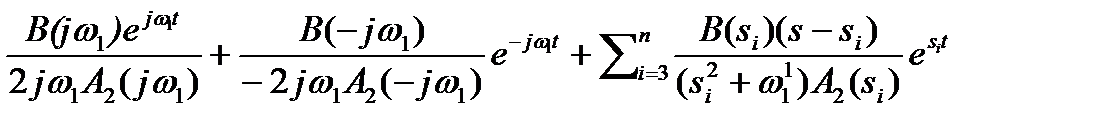 .
.
Первые два слагаемых в правой части этого равенства являются комплексно-сопряженными величинами, при сложении их вещественные части удвоятся, а мнимые уничтожатся,
x (t) = Re 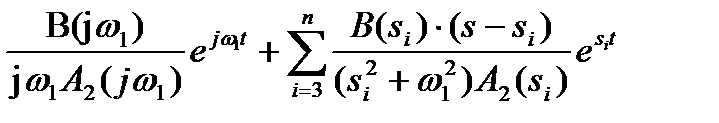 .
.
Пример 1.
Найти импульсную функцию для 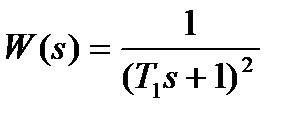 мпульсная функция определяется, как
мпульсная функция определяется, как 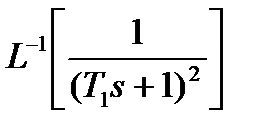 . Изображение имеет единственный полюс
. Изображение имеет единственный полюс 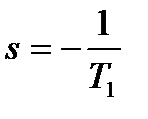 к кратности
к кратности 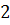 . Получим
. Получим
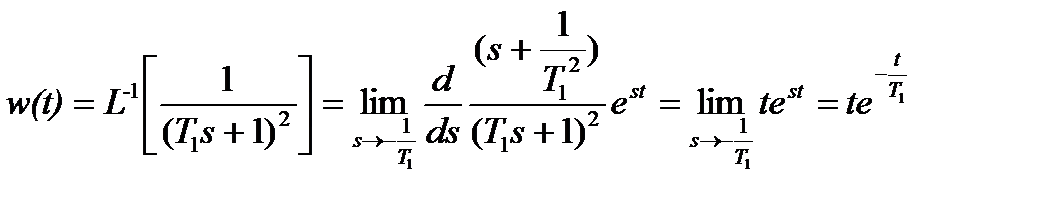
Пример 2.
Найти импульсную функцию для 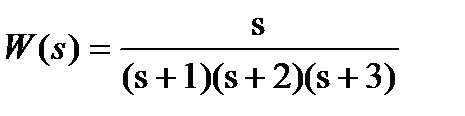 .
.
Импульсная функции 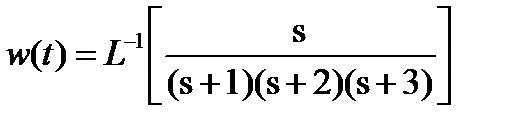 .
.
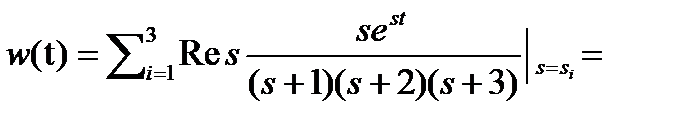
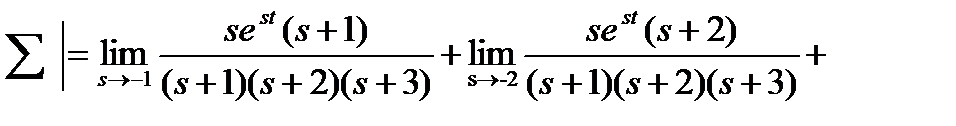
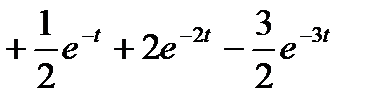
Пример 3.
Найти импульсную характеристику колебательного звена 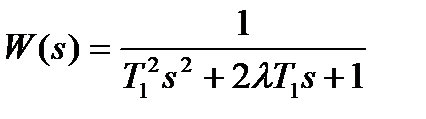 .
.
Импульсная функция 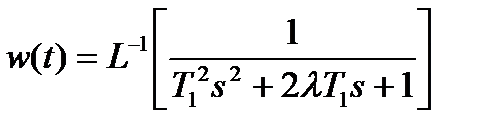 .
.
Полюса W(s) имеют кратность 1 и являются комплексно-сопряженными
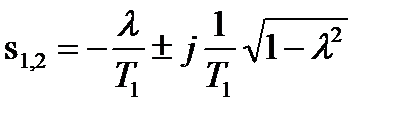
На основании формулы 9 получим:
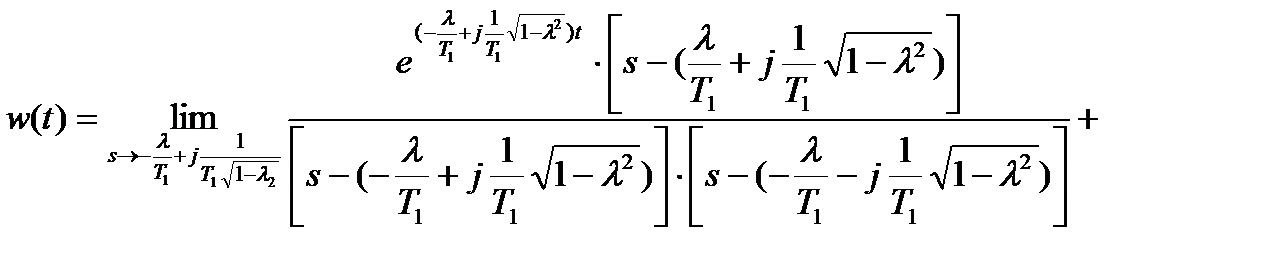
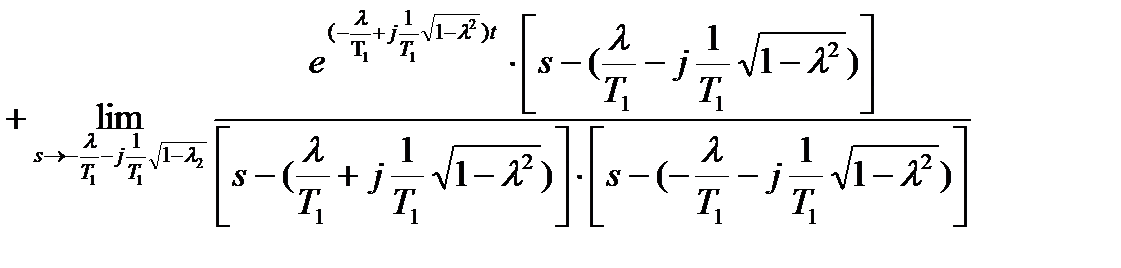 .
.
Выполнив сокращение одинаковых сомножителей в числителе и знаменателе, выносим одинаковый для обоих слагаемых множитель 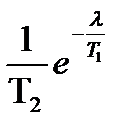 получим:
получим:

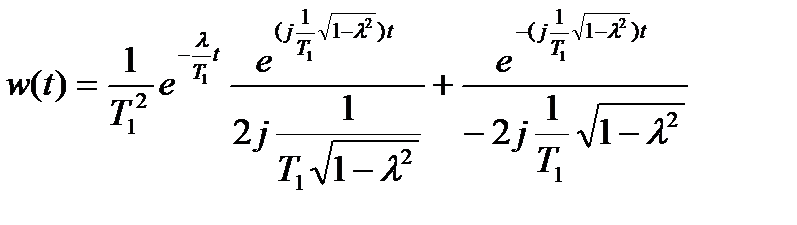
учитывая, что 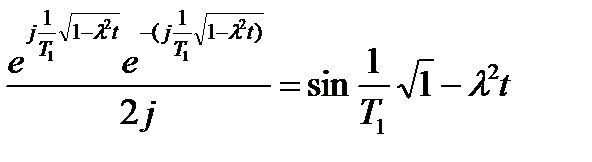 ,
,
окончательно получим:
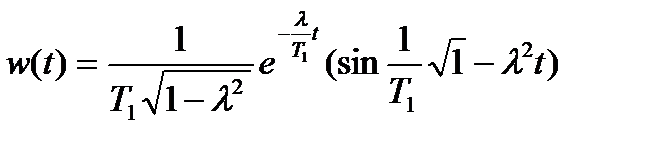
Второй способ нахождения оригинала x (t) по известному изображению X (s) заключается в разложении изображения 
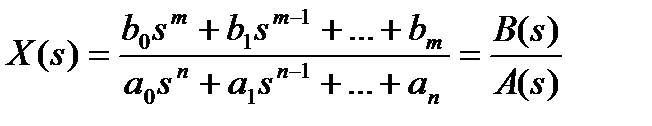 , m < n на простые дроби.
, m < n на простые дроби.
Это разложение правильной дроби на простые дроби связано с разложением её знаменателя 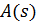 на простые множители. Каждый целый многочлен с вещественными коэффициентами разлагается единственным способом на вещественные множители вида
на простые множители. Каждый целый многочлен с вещественными коэффициентами разлагается единственным способом на вещественные множители вида 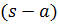 и
и 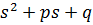 при этом квадратные множители предполагаются не имеющими вещественных корней и, следовательно, неразложимыми на вещественные линейные множителями. Вынося старший коэффициент многочлена
при этом квадратные множители предполагаются не имеющими вещественных корней и, следовательно, неразложимыми на вещественные линейные множителями. Вынося старший коэффициент многочлена 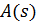 можно записать разложение этого многочлена в виде:
можно записать разложение этого многочлена в виде:
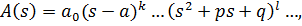
где 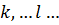 натуральные числа.
натуральные числа.
В алгебре устанавливается, что каждому множителю вида 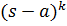 в разложении знаменателя правильной дроби отвечает группа из
в разложении знаменателя правильной дроби отвечает группа из 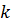 простых дробей:
простых дробей:

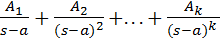 ,
,
а каждому множителю вида (s2+ ps + q) l - группа из l простых дробей:
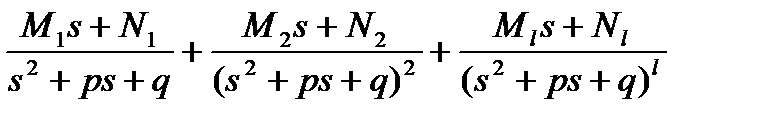
причем 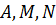 - числовые вещественные коэффициенты.
- числовые вещественные коэффициенты.
Значение этих коэффициентов определяются следующим образом. Зная форму разложения дроби 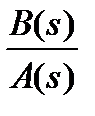 выполняют операцию сложения. В результате получаем дробь, знаменатель которой равен A (s), а числитель будет представлять многочлен степени не больше
выполняют операцию сложения. В результате получаем дробь, знаменатель которой равен A (s), а числитель будет представлять многочлен степени не больше 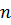 , с коэффициентами, зависимыми от A 1, A 2… Ak, M 1… Ml, N 1… Nl. Приравнивая коэффициенты при одинаковых степенях
, с коэффициентами, зависимыми от A 1, A 2… Ak, M 1… Ml, N 1… Nl. Приравнивая коэффициенты при одинаковых степенях 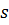 этого многочлена к коэффициентам многочлена
этого многочлена к коэффициентам многочлена 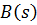 получим систему линейных уравнений относительно искомых коэффициентов. Решение этой системы даст численные значения коэффициентов.
получим систему линейных уравнений относительно искомых коэффициентов. Решение этой системы даст численные значения коэффициентов.
Пусть дано рациональное выражение 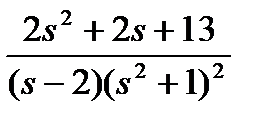 .
.
Её разложение на простые дроби будет иметь вид:
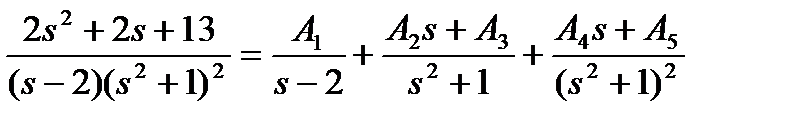
Коэффициенты A 1, A 2, A 3, A 4, A 5 определяем исходя из равенства
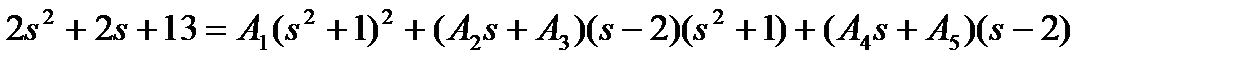 .
.
Приравнивая коэффициенты при одинаковых степенях 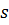 слева и справа получим систему из пяти уравнений.
слева и справа получим систему из пяти уравнений.
s4 A 1+ A 2
s3 -2 A 2+ A 3=0
s2 2 A 1+ A 2-2 A 3+ A 4=2
s1 -2 A 2+ A 3-2 A 4+ A 5=13
s0 A 1+2 A 3-2 A 5+ A 5=13
Откуда A 1=1, A 2=-1, A 3=-2, A 4=-3, A 5=13.
Окончательно
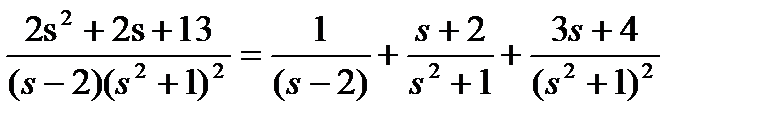
 Теперь чтобы найти оригинал от изображения
Теперь чтобы найти оригинал от изображения 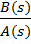 надо найти оригинал от каждой из простых дробей и полученные оригиналы сложить. Для нахождения оригиналов от простых дробей можно воспользоваться таблицей соответствия между оригиналами и изображениями.
надо найти оригинал от каждой из простых дробей и полученные оригиналы сложить. Для нахождения оригиналов от простых дробей можно воспользоваться таблицей соответствия между оригиналами и изображениями.
Пример 4.
Найти переходную функцию для 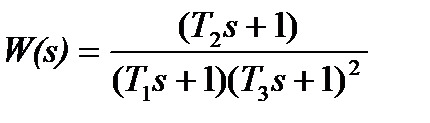 .
.
Переходная функция определяется как:
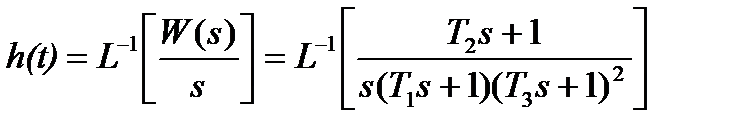 .
.
Представим 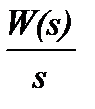 в виде суммы простых дробей.
в виде суммы простых дробей.
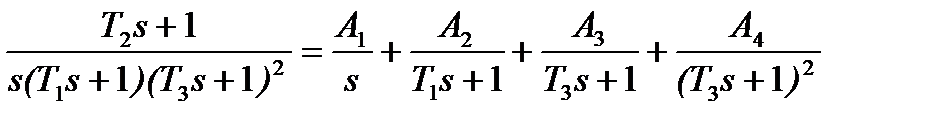
Коэффициенты А1, А2, А3, А4 найдем из тождества:
T 2 s+ 1 =A 1 (T 1 s+ 1 )(T 3 s+ 1 ) 2 +A 2 s(T 3 s+ 1 ) 2 +A 3 s(T 1 s+ 1 )(T 3 s+ 1 )+A 4 s(T 1 s+ 1 )
Откуда:
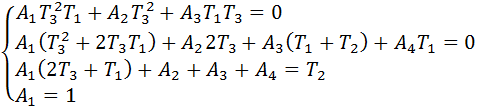
Предположим, что для заданных значений 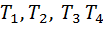 определено численное значение
определено численное значение 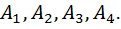 Пользуясь таблицей соответствия между изображениями и оригиналами найдём
Пользуясь таблицей соответствия между изображениями и оригиналами найдём
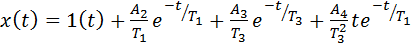 .
.
 2015-06-05
2015-06-05 1486
1486
