Построение корневых годографов

В большинстве случаев характеристическое уравнение исследуемой системы представимо в виде

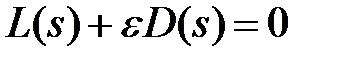(1)

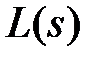где и 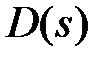полиномы комплексного переменного s, 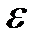- некоторый параметр, который в дальнейшем будем называть варьируемым. (Таким параметром может служить, например, передаточный коэффициент k разомкнутой системы).

Траектории, которые описывают корни характеристического уравнения на плоскости S при изменении параметра 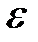системы от 0 до ∞ получили название корневых годографов. Построенные корневые годографы позволяют вычислить, как влияет на устойчивость и динамические характеристики системы изменение варьируемого параметра.

Имея характеристическое уравнение (1) с известными нулями входящих в него полиномов L (s) и D (s) можно приблизительно построить на плоскости S корневые годографы.

Для этого (1) переписываем в виде:

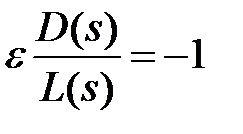(2)

Учитывая, что s - комплексная переменная, (2) можно записать в виде двух уравнений: уравнения аргументов

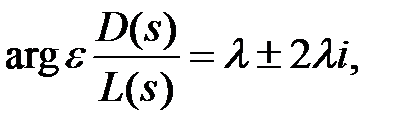π + 2πi, 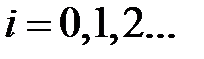, (3)

и уравнения модулей

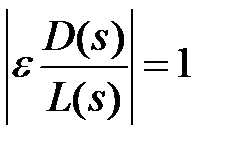. (4)

Представим 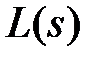и 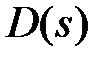в виде:

,

,

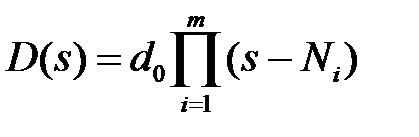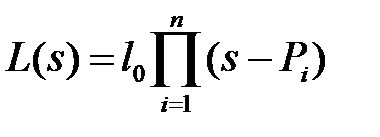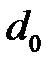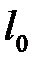где и - коэффициент при s наивысшей степени,

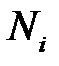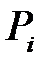, - нули полиномов 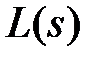и ,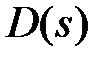

m и n – порядки полиномов 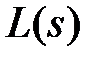и .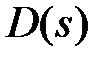

Уравнение аргументов (3) можно переписать в следующем виде:

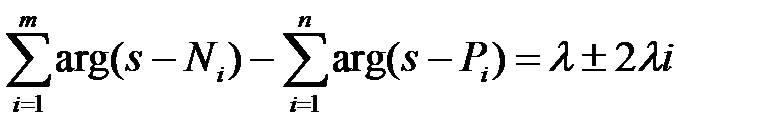π + 2πi (5)

Из выражения (5) следует: точка s плоскости S принадлежит корневому годографу, если сумма аргументов векторов, проведенных из нулей функции 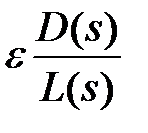в эту точку, за вычетом суммы аргументов векторов, проведенных из полюсов 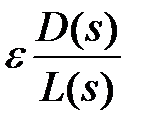в эту же точку, равно π + 2πi.

(Сказанное показано на рис.1)

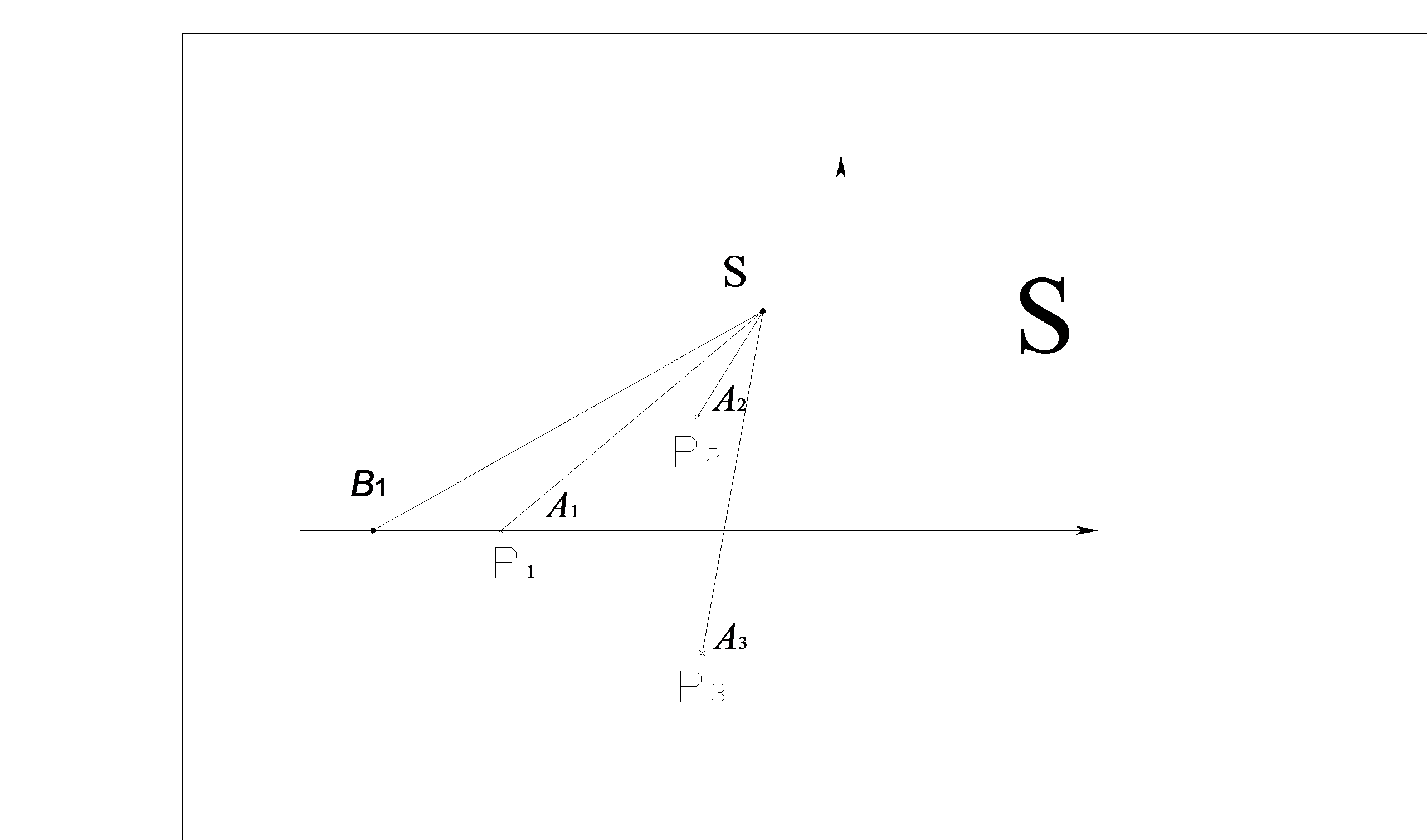
Рис. 1.

На этом рисунке через 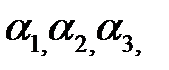обозначены аргументы векторов, проведенных из полюсов 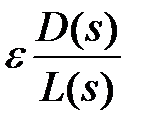, 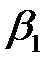аргумент вектора, проведенного из нуля .

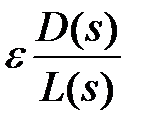На основании выражения (5) можно сформулировать следующие основные правила построения корневых годографов:

1. Вещественная ось плоскостей S является осью симметрии для корневых годографов и для асимптот корневых годографов.

2. При изменении 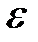от 0 до ∞ корневые годографы выйдя из полюсов функции 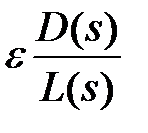, должны прийти в нули 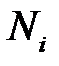функции .

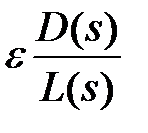Если число полюсов n больше числа нулей m, то (n-m) ветвей корневого годографа уйдут в бесконечность. Если число нулей больше числа полюсов, то (n-m) ветвей корневого годографа придут из бесконечности.

3. Ветви корневых годографов, находящихся в бесконечности имеют асимптоты. Число асимптот равно 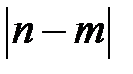. Асимптоты пересекаются в одной точке 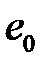вещественной оси плоскости S, причем:

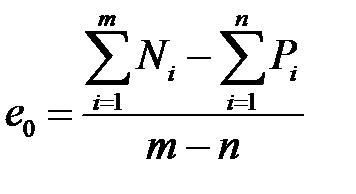, (6)

и имеют углы наклона 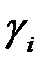относительно положительного направления вещественной оси плоскости S:

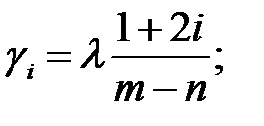π 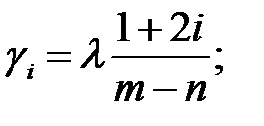, i =0,1,2…| m-n |-1. (7)

4. Точки вещественной оси плоскости S справа от которых находится нечетное число нулей и полюсов функции 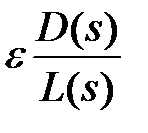обязательно принадлежат корневым годографам, а точки этой оси справа от которых находится четное число нулей и полюсов не могут принадлежать корневым годографам.

5. В некоторых точках вещественной оси плоскости S, принадлежащих корневым годографам, корневые годографы могут, встретившись, разойтись, один в верхнюю, а другой в нижнюю части плоскости S.

Сформулированные выше правила позволяют приближенно выполнить построение корневых годографов.

Рассмотрим некоторые примеры построения корневых годографов.

Построить корневые годографы для варьируемого параметра К для замкнутой системы, если передаточная функция разомкнутой системы:

Пример 1.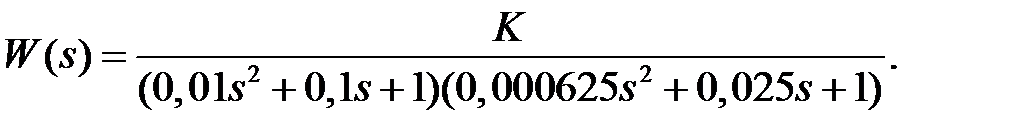

Решение: Характеристическое уравнение замкнутой системы 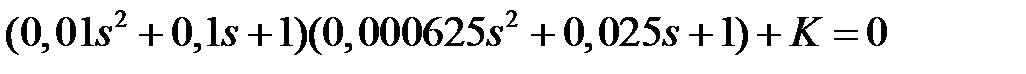. Представим его в виде 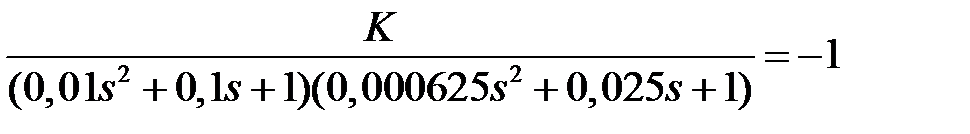. Отсюда видно, что количество нулей равно 0, а количество полюсов равно 4. Их значения можно получить, найдя корни знаменателя. Получаем

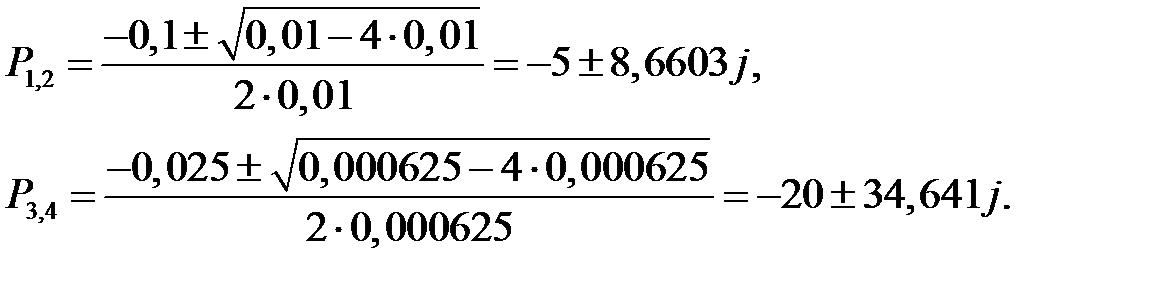
Наносим полюса на комплексную плоскость. В соответствии с правилом 2 все корневые годографы должны уйти в бесконечность. Число асимптот равно 4-0=4. Определим точку, расположенную на вещественной оси, в которой пересекаются асимптоты 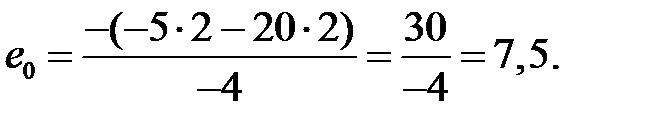–7,5

Определим углы, которые асимптоты составляют с положительным направлением вещественной оси (правило 3).

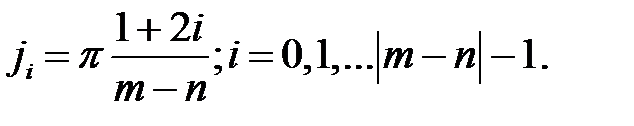
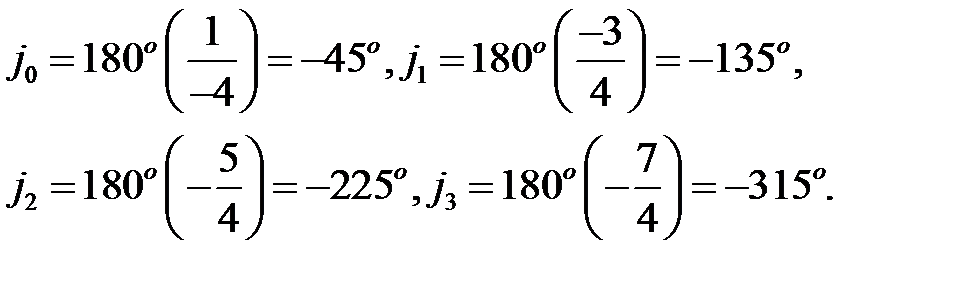
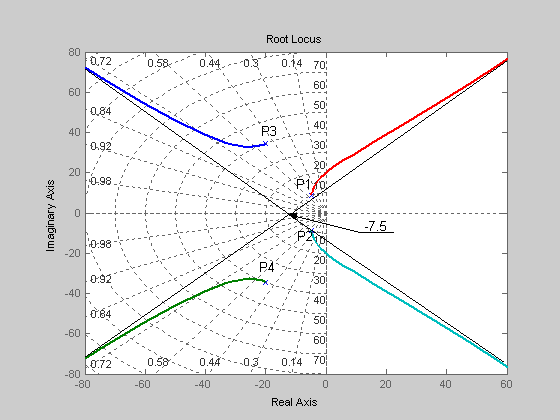
Наносим асимптоты на комплексную плоскость, как показано на рис.2. На этом же рисунке показаны корневые годографы, которые выходят из полюсов и уходят в бесконечность, неограниченно приближаясь к нарисованным асимптотам.

Рис.2

Пример 2.

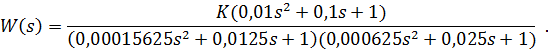
Решение: Характеристическое уравнение замкнутой системы имеет вид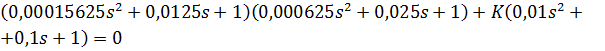

Отсюда .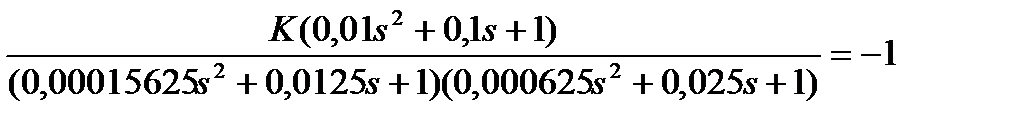

Приравнивая к нулю числитель и знаменатель, получим нули и полюса корневых годографов

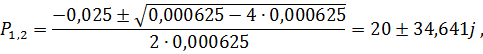
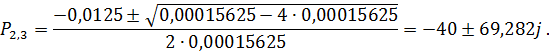
Наносим полюса 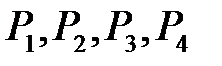и нули 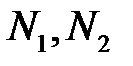на комплексную плоскость, как показано на рис.2. В соответствии с правилом 1, два корневых годографа должны закончиться в бесконечности, кроме того в соответствии с правилом 4 ни одна из точек вещественной плоскости не принадлежит корневым годографам.

В соответствии с правилом 3, корневые годографы имеют 2 асимптоты, пересекающиеся с вещественной осью в точке

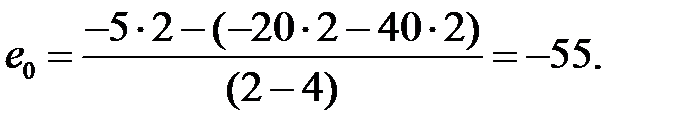
Углы между асимптотами и положительным направлением вещественной оси будут равны (правило 3)

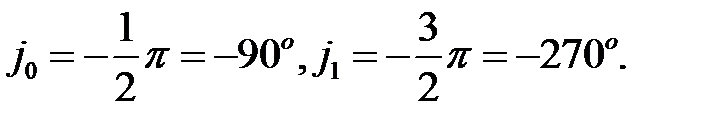
С учетом сказанного корневые годографы будут иметь вид, показанный на рис.3. Корневые годографы выйдя из полюсов P₁ и P₂ закончатся в нулях N₁ и N₂. Корневые годографы выйдя из полюсов P₃ и P₄ уйдут в бесконечность неограниченно приближаясь к асимптотам, пересекающим вещественную ось в точке –55.

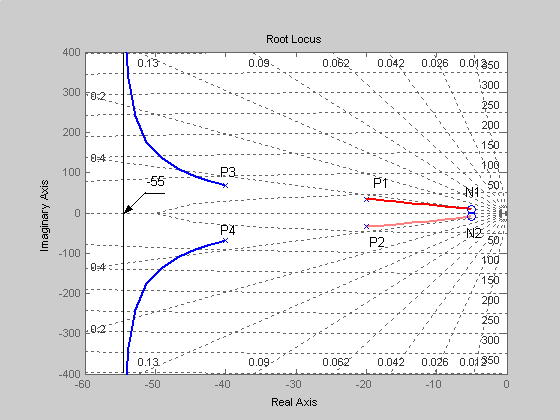
Рис.3

Пример 3.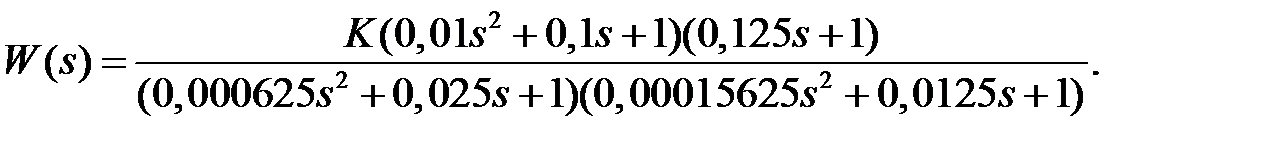

Решение: Характеристическое уравнение замкнутой системы

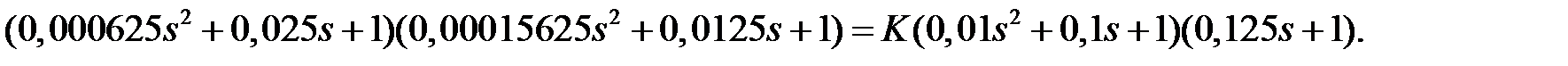Представим его в виде

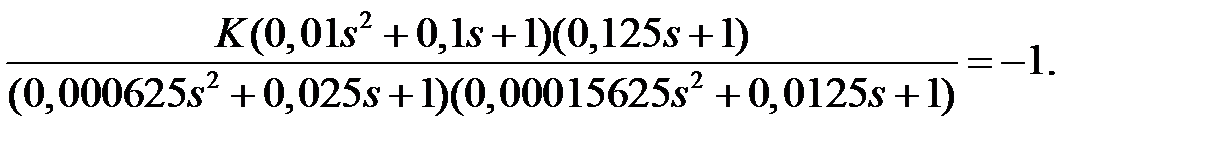
Нули корневых годографов будут:

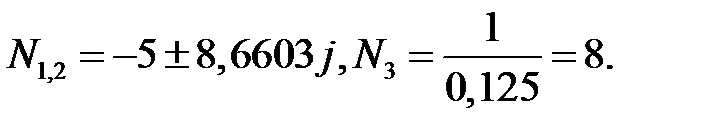
Полюса корневых годографов будут:

Наносим нули и полюса на комплексную плоскость, как показано на рис. 4. В соответствии с правилом 4, часть вещественной оси, лежащая левее нуля N₃ будет принадлежать корневым годографам, при этом этот отрезок оси является асимптотой для годографа, уходящего в бесконечность.

Корневые годографы, построенные в соответствии с изложенными выше правилами, изображены на том же рисунке. Два корневых годографа, выйдя из полюсов P₁ и P₂ придут в нули N₁ и N₂. Корневые годографы, выйдя из полюсов P₃ и P₄ сойдутся в одной точке на вещественной оси, равной примерно 84 и, затем один закончится нуле N₃, а другой уйдет в бесконечность.

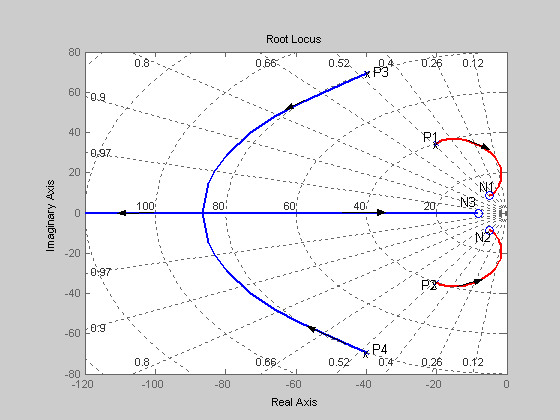
Рис.4