2015-04-12
11714
Важнейшим понятием аналитической геометрии является уравнение линии на плоскости.
Определение. Уравнением линии (кривой) на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии (рис.1).
Рис.1.
В общем случае уравнение линии может быть записано в виде F(x,y)=0 или y=f(x).
Пример. Найти уравнение множества точек, равноудаленных от точек А(-4;2), B(-2;-6).
Решение. Если M(x;y) – произвольная точка искомой линии (рис.2), то имеем AM=BM или
.
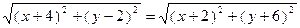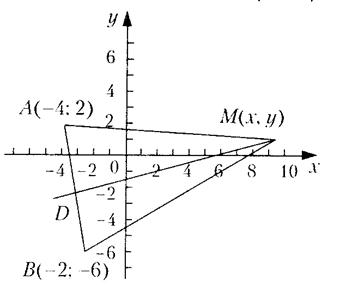
Рис.2.
После преобразований получим
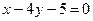или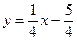 
.
Очевидно, что это уравнение прямой MD – перпендикуляра, восстановленного из середины отрезка AB.
Из всех линий на плоскости особое значение имеет прямая линия. Она является графиком линейной функции, используемой в наиболее часто встречающихся на практике линейных экономико-математических моделях.
Различные виды уравнения прямой:
1)с угловым коэффициентом k и начальной ординатой b:
y = kx + b,
где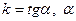 
– угол между прямой и положительным направлением оси ОХ (рис. 3).
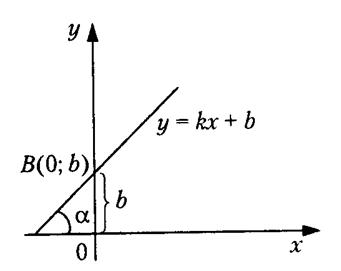
Рис.3.
Особые случаи:
– прямая проходит через начало координат (рис.4):
y = kx;
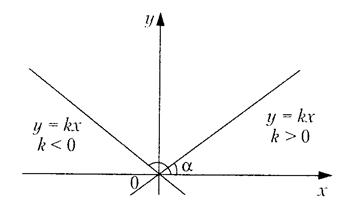
Рис. 4.
– биссектриса первого и третьего, второго и четвертого координатных углов:
y=+x, y=-x;
– прямая параллельна оси ОХ и сама ось ОХ (рис. 5):
y=b, y=0;
Рис.5.
– прямая параллельна оси OY и сама ось ОY (рис. 6):
x=a, x=0;
Рис.6.
2) проходящей в данном направлении (с угловым коэффициентом) k через данную точку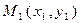 
(рис. 7) :
.
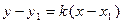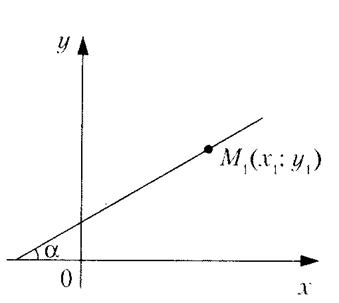
Рис.7.
Если в приведенном уравнении k – произвольное число, то уравнение определяет пучок прямых, проходящих через точку , кроме прямой 
, параллельной оси Oy.
Пример. Составить уравнение прямой, проходящей через точку А(3,-2):
а) под углом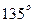 
к оси ОХ;
б) параллельно оси OY.
Решение.
а)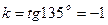 
, y-(-2)=-1(x-3) или y=-x+1;
б) х=3.
3) проходящей через две данные точки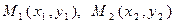 
(рис. 8) :
.
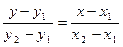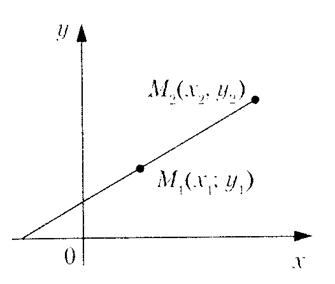
Рис. 8.
Пример. Составить уравнение прямой, проходящей через точки А(-5,4), В(3,-2).
Решение.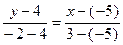 
,
.
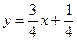4) уравнение прямой в отрезках (рис.9):
,
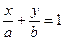где a, b – отрезки, отсекаемые на осях соответственно Ox и Oy.
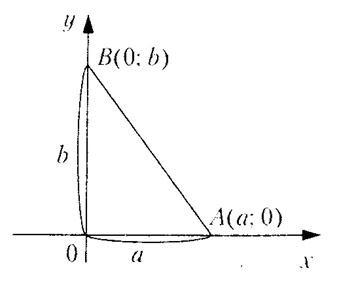
Рис. 9.
Пример. Составить уравнение прямой, проходящей через точку А(2,-1), если эта прямая отсекает от положительной полуоси Oy отрезок, вдвое больший, чем от положительной полуоси Ox (рис. 10).
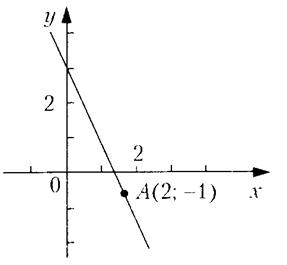
Рис. 10.
Решение. По условию b=2a, тогда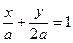 
. Подставим координаты точки А(2,-1):
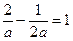, откуда a=1,5.
Окончательно получим:
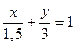или y=-2x+3.
5) общее уравнение прямой:
Ax+By+C=0,
где a и b не равны одновременно нулю.
Некоторые важные характеристики прямых:
1) расстояние d от точки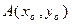 
до прямой:
.
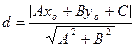2) угол 
между прямым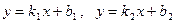и 
[1] и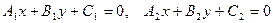 
соответственно:
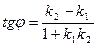и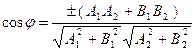 
.
3) условие параллельности прямых:
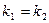или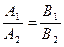 
.
4) условие перпендикулярности прямых:
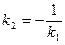или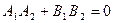 
.
Пример 1. Составить уравнение двух прямых, проходящих через точку А(5,1), одна из которых параллельна прямой 3x+2y-7=0, а другая перпендикулярна той же прямой. Найти расстояние между параллельными прямыми.
Решение. Рисунок 11.
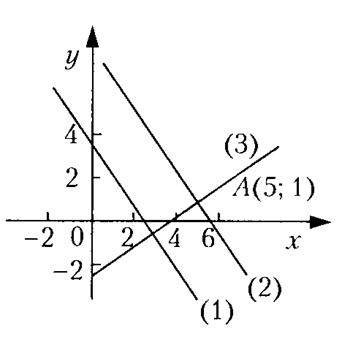
Рис. 11.
1) уравнение параллельной прямой Ax+By+C=0:
из условия параллельности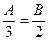 
;
взяв коэффициент пропорциональности, равный 1, получим А=3, В=2;
т.о. 3x+2y+C=0;
значение С найдем, подставив координаты т. А(5,1),
3*5+2*1+С=0, откуда С=-17;
уравнение параллельной прямой – 3x+2y-17=0.
2) уравнение перпендикулярной прямой из условия перпендикулярности будет иметь вид 2x-3y+C=0;
подставив координаты т. А(5,1), получим 2*5-3*1+С=0, откуда С=-7;
уравнение перпендикулярной прямой – 2x-3y-7=0.
3) расстояние между параллельными прямыми можно найти как расстояние от т. А(5,1) до дано прямой 3x+2y-7=0:
.
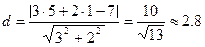Пример 2. Даны уравнения сторон треугольника:
3x-4y+24=0 (AB), 4x+3y+32=0 (BC), 2x-y-4=0 (AC).
Составить уравнение биссектрисы угла АВС.
Решение. Вначале найдем координаты вершины В треугольника:
,
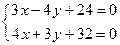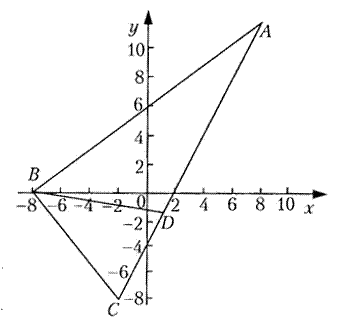
откуда x=-8, y=0, т.е. В(-8,0) (рис. 12).
Рис. 12.
По свойству биссектрисы расстояния от каждой точки M(x,y), биссектрисы BD до сторон АВ и ВС равны, т.е.
,
.
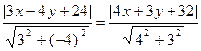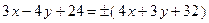Получаем два уравнения
x+7y+8=0, 7x-y+56=0.
Из рисунка 12 угловой коэффициент искомой прямой отрицательный (угол с Ох тупой), следовательно, нам подходит первое уравнение x+7y+8=0 или y=-1/7x-8/7.
