Использование формулы Бернулли при больших n и m вызывает трудности из-за громоздких вычислений => возникает необходимость в отыскании вероятности 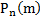 обеспечивающих необходимую точность.
обеспечивающих необходимую точность.
Теорема: если число испытаний неограниченно увеличивается n 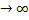 и вероятность р наступления соб.А в каждом испытании уменьшается р
и вероятность р наступления соб.А в каждом испытании уменьшается р 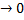 , но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность
, но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность 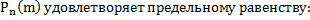
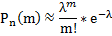
Доказательство: λ=np => p=λ/n подставляем это равенство в формулу: 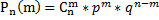
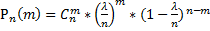 =
= 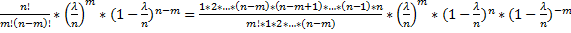 =
= 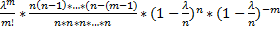 =
= 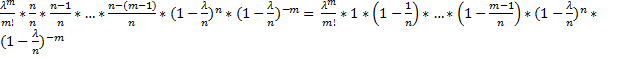
Перейдем к пределу в обеих частях неравенства при n 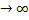 :
:
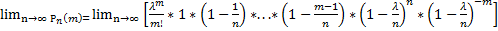
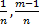 ,
, 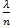
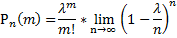
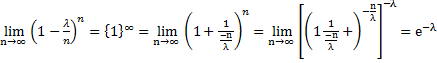 =>
=> 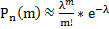
Формулу Пуассона применяют обычно когда n≥50, np≤10
Пример: Крымский завод отправил в Москву 1500 бутылок вина; вероятность того, что в пути бутылка может разбиться = 0,002. Найти вероятность того, что будет разбито в пути 4 бутылки.
Решение: 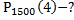
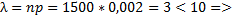 з-н Пуассона
з-н Пуассона
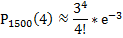
 2015-06-05
2015-06-05 870
870








