2015-06-04
294
(внесение под знак дифференциала)
При интегрировании подстановкой вводится новая переменная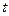 
, связанная с 
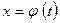с таким расчётом, чтобы получить один из табличных интегралов. Найдя интеграл по новой переменной, надо возвратиться к первоначальной переменной.
Указать общее правило для выбора подстановки нельзя, т.к. этот выбор в каждом отдельном случае зависит от вида подынтегральной функции.
В простых случаях при введении новой переменной рекомендуется применять следующие преобразования дифференциала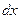 
:
|
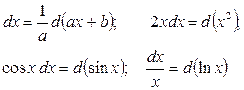
Пример 1. Найти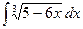 
.
Решение (I способ): среди табличных интегралов подходящего нет, но по формуле (3) табличных интегралов можно вычислить интеграл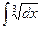 
, сходный с данным. Поэтому пробуем ввести вспомогательную переменную 
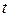, связанную с 
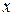зависимостью:
|
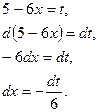
Подынтегральное выражение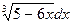 
с помощью (â) и (ââ) преобразуется к виду 
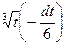, и получим:
= 
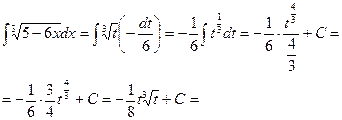
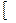
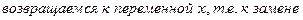(â)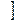 
=
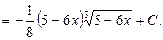
(II способ): данный интеграл можно вычислить и другим способом – внесением под знак дифференциала. В качестве вспомогательной была выбрана следующая функция: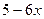 
. Находим её дифференциал: 
.
|
|
|
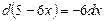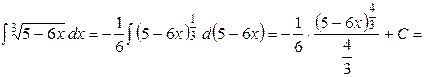
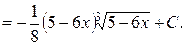
Пример 2. Найти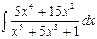 
.
Решение (I способ):
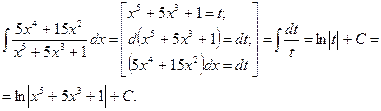
( II способ ). Заметим, что числитель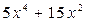 
равен производной знаменателя 
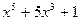, т.е.
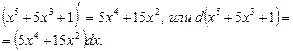
Имеем:
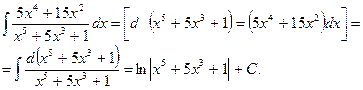
Пример 3. Найти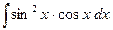 
.
Решение (I способ):
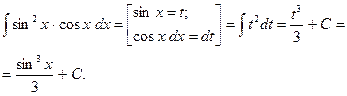
(II способ):
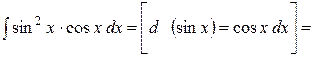
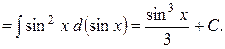
Пример 4. Найти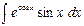 
.
Решение (I способ):
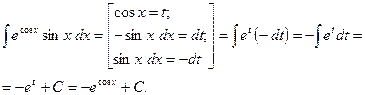
(II способ):
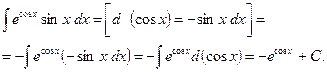
Пример 5. Найти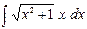 
.
Решение (I способ):
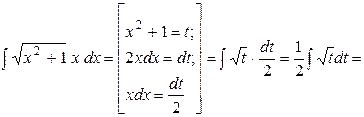
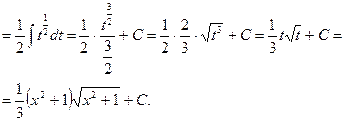
(II способ):
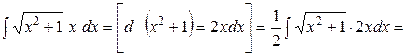
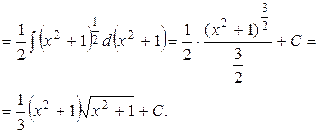
Обратим внимание на вычисление некоторых интегралов, часто встречающихся на практике.
Пример 6. Найти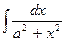 
.
Решение.
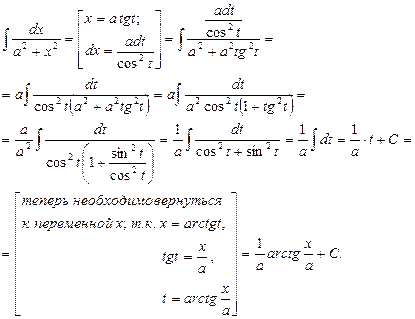
Пример 7.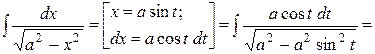 
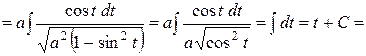
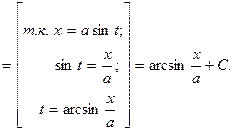
Пример 8. Найти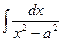 
.
Решение.
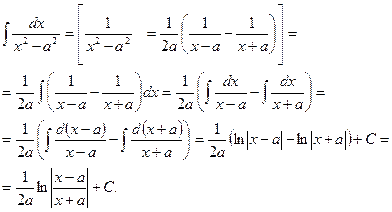
Пример 9.
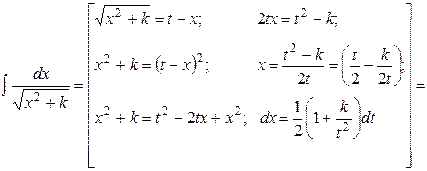
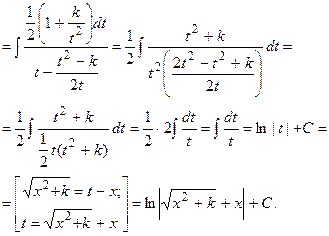
Пример 10.
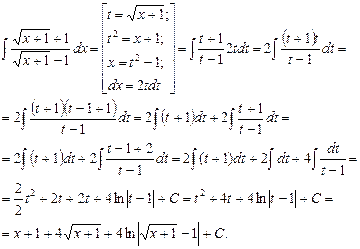
Пример 11.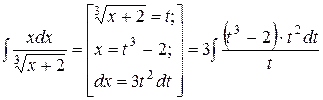 
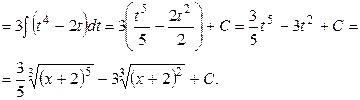
Теперь мы можем расширить таблицу интегралов.
| Формула | № |
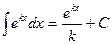
| (6а) |
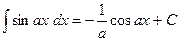
| (7а) |
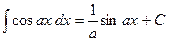
| (8а) |
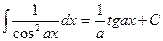
| (9а) |
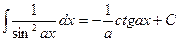
| (10а) |
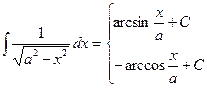
| (11а) (12a) |
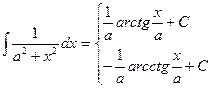
| (13а) (14a) |
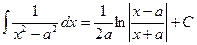
| (15) |
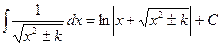
| (16) |
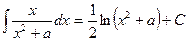
| (17) |
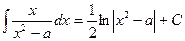
| (17а) |
