Функция, заданная в виде отношения двух многочленов
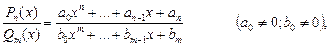
называется рациональной функцией или рациональной дробью.
Если 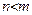 рациональная дробь называется правильной; в противном случае – неправильной.
рациональная дробь называется правильной; в противном случае – неправильной.
Если дробь неправильная, то нужно выделить целую рациональную часть, используя алгоритм деления многочленов “углом”, и представить исходную дробь в виде суммы целой рациональной функции и правильной дроби.
Пример 1. Выделить целую часть дроби: 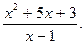
Решение:
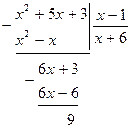
Таким образом, 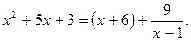
Любая правильная рациональная дробь может быть разложена на сумму конечного числа простейших рациональных дробей. Различают четыре типа таких дробей:
1) 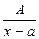 ; 2)
; 2) 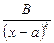 ; 3)
; 3) 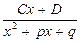 ; 4)
; 4) 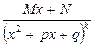 ,
,
при этом предполагается, что трехчлен 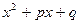 не имеет вещественных корней.
не имеет вещественных корней.
Рассмотрим интегрирование дробей первых трёх указанных типов
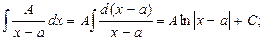
|
|
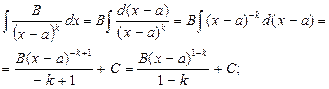
|
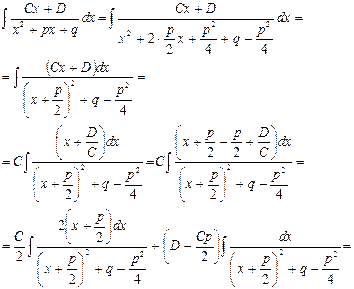
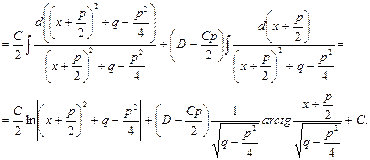
Четвертый тип вычисляется с использованием понижения степени k.
Всякий многочлен с вещественными коэффициентами степени выше второй разлагается на линейные и квадратные множители с вещественными коэффициентами.
Каждому неповторяющемуся множителю вида 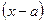 отвечает в разложении простая дробь
отвечает в разложении простая дробь 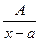 , каждому множителю
, каждому множителю 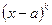 отвечает сумма k простых дробей вида:
отвечает сумма k простых дробей вида:
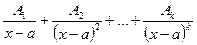 .
.
Неповторяющемуся множителю 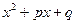 отвечает одна простая дробь
отвечает одна простая дробь 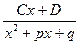 , где A1, A2, …, Ak, C,D - числовые коэффициенты.
, где A1, A2, …, Ak, C,D - числовые коэффициенты.
Для определения последних коэффициентов прибегают к методу неопределенных коэффициентов, который состоит в следующем:
1) записывают дробь 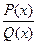 в виде суммы простых дробей; дроби приводят к общему знаменателю; умножают обе части равенства на
в виде суммы простых дробей; дроби приводят к общему знаменателю; умножают обе части равенства на 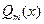 , вследствие чего получают равенство двух многочленов - слева многочлен
, вследствие чего получают равенство двух многочленов - слева многочлен 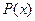 с известными коэффициентами, а справа многочлен с неизвестными коэффициентами;
с известными коэффициентами, а справа многочлен с неизвестными коэффициентами;
2) приравняв у них коэффициенты при одинаковых степенях x,получают систему линейных алгебраических уравнений.
Пример 2. Разложить на простые дроби следующую дробь: 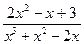 .
.
Решение: 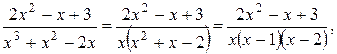
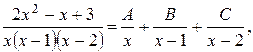
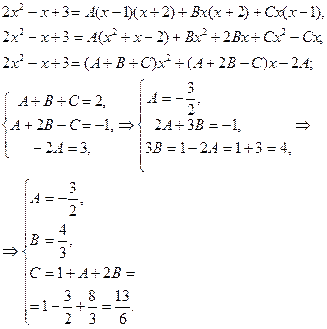
Таким образом,
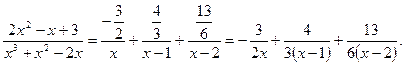
Пример 3. Разложить на простые дроби следующую дробь:
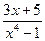 .
.
Решение:
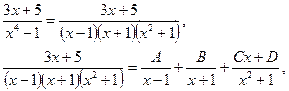
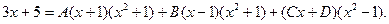 (â)
(â)
В рассматриваемом примере некоторые коэффициенты можно определить методом частных значений. Для этого положим, 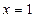 ,
, 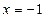 и подставим вместо x их в равенство (â)
и подставим вместо x их в равенство (â)
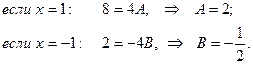
Для определения C и D сравним коэффициенты при х2 и х3.
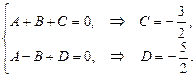
Таким образом, 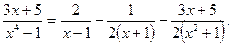
Пример 4. Найти интеграл: 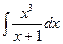 .
.
Решение: подынтегральная дробь – неправильная. Выделим целую часть; для этого делим числитель на знаменатель:
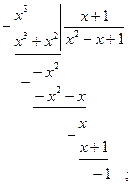
|
Имеем:
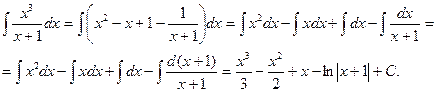
Пример 5. Найти интеграл: 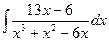 .
.
Решение. Данная дробь – правильная. Разлагаем знаменатель на множители:
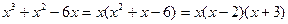 .
.
Числитель не делится ни на один из этих множителей, так что дробь не сокращается. Все множители – первой степени и ни один не повторяется.
Способом, указанным в примере 2, находим 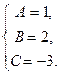
Получаем:
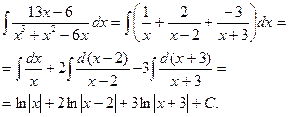
Пример 6. Найти интеграл: 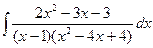 .
.
Решение. Представим дробь в виде суммы дробей и определим коэффициенты способом, указанным в примерах 2, 3:
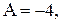
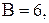
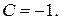
Получаем разложение данного интеграла:
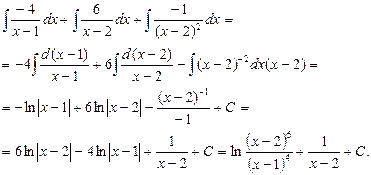
 2015-06-04
2015-06-04 1378
1378

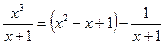 .
. 






