Интегрирование по частям

Интегрирование по частям производится по формуле:

,

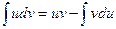где 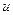и 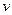– функции переменной интегрирования, например, .

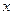Применяя эту формулу, приходится разбивать подынтегральное выражение на два множителя: 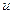и 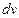; первый из них (т.е. 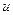) затем дифференцируется, а второй (т.е. 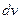) интегрируется. В результате получается упрощённое подынтегральное выражение.

Методом интегрирования по частям следует пользоваться в тех случаях, когда подынтегральная функция имеет вид:

1) -
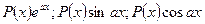в этом случае за 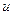принимают многочлен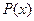

2) -
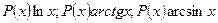в этом случае за 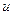принимают трансцендентную функцию.

Пример 1. Найти .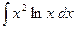

Решение.

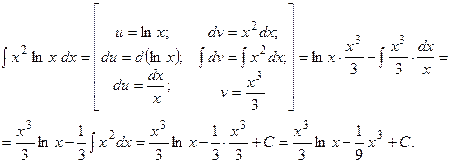
Пример 2. Найти .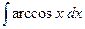

Решение.

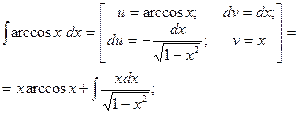
находим:

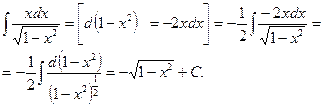
Таким образом,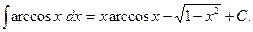

Пример 3. Найти .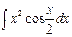

Решение.

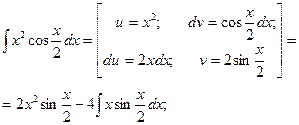
вычислим интеграл 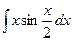, еще раз применив формулу интегрирования по частям, т.е.

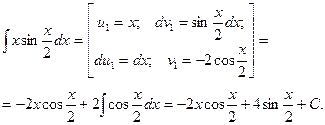
имеем: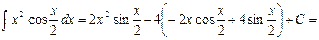

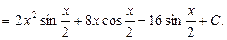
Пример 4.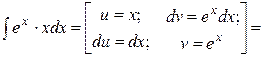

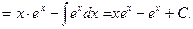
Пример 5. Найти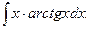

Решение.

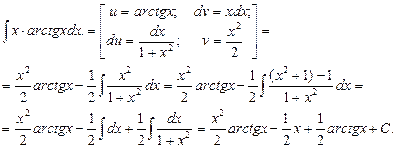
Иногда повторное интегрирование по частям приводит заданный интеграл к самому себе. В этом случае может получиться или ничего не дающее тождество, или такое уравнение первой степени относительно искомого интеграла, из которого находится заданный интеграл. Проиллюстрируем это примером.

Пример 6. Найти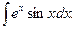

Решение.

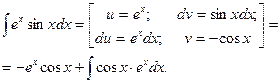
Для нахождения последнего интеграла интегрируем еще раз по частям: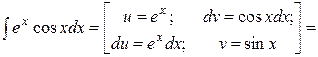

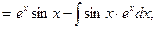
т.е.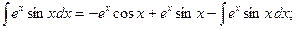

последний интеграл такой же, как данный; перенесем его в левую часть равенства:

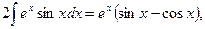
откуда: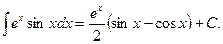

Существует много функций, которые не относятся к вышеназванным, но тоже интегрируются по частям.

Пример 7.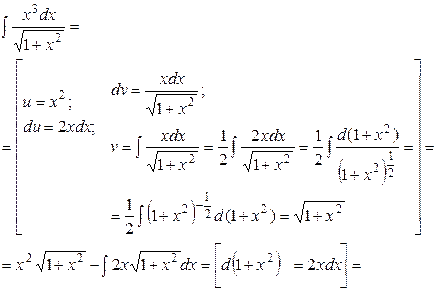

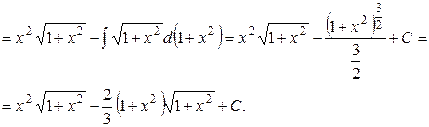
Этот интеграл можно вычислить и другим способом, используя подстановку 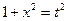, (â)

тогда:

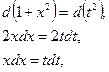
из (â):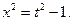

Имеем:

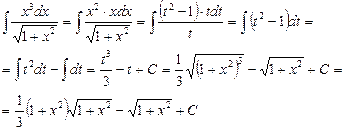
Пример 8.