Основным методом при интегрировании тригонометрических функций является метод подстановки.
1. Если подынтегральная функция нечетна относительно 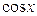 , применяется подстановка
, применяется подстановка 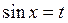 .
.
Пример 1. Найти 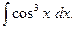
Решение.
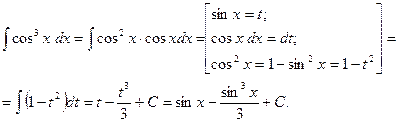
2. Если подынтегральная функция нечетна относительно 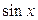 , применяется подстановка
, применяется подстановка 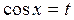 .
.
Пример 2. 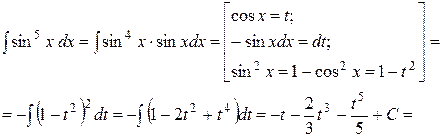
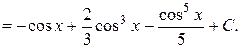
3. Интегралы вида 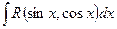 с помощью подстановки
с помощью подстановки 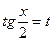 сводятся к интегралам от рациональной функции.
сводятся к интегралам от рациональной функции.
Выразим 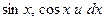 через
через 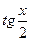 :
:
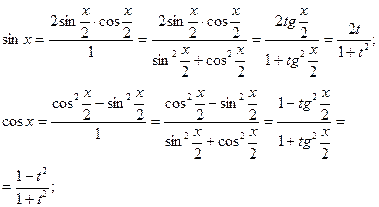
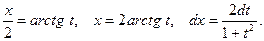
Таким образом, 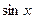
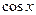 и
и 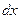 выразились рационально через
выразились рационально через 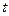 . Подставим полученные выражения в интеграл, получим интеграл от рациональной функции:
. Подставим полученные выражения в интеграл, получим интеграл от рациональной функции:
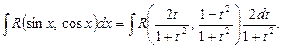
Пример 3. 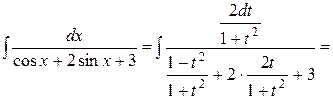
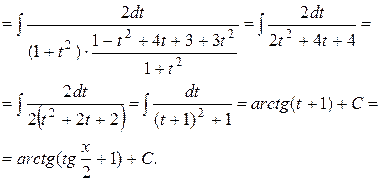
4. Если подынтегральная функция имеет вид 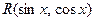 , но
, но 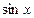 и
и 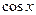 входят только в четных степенях, то применяется подстановка:
входят только в четных степенях, то применяется подстановка: 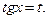 .
.
sin2 x, cos2 x и dx рационально выражаются через 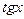 :
:
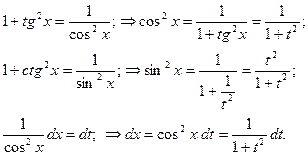
После подстановки получим интеграл от рациональной функции.
Пример 4. Найти 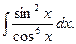
Решение.
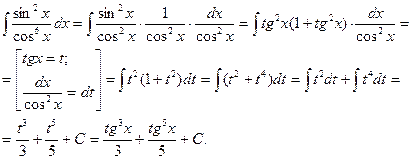
 2015-06-04
2015-06-04 270
270








