Нормальное распределение (распределение Гаусса)

С увеличением 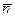распределение Пуассона становится всё более симметричным относительно 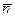, а относительная дискретность событий становится практически незаметной. Для больших значений 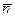, распределение Пуассона переходит в распределение Гаусса

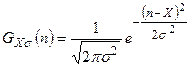. (4.23)

Функция 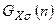называется также функцией Гаусса. Говорят, что результаты измерений имеют нормальное распределение, если они описываются функцией Гаусса.

Распределение Гаусса является симметричным, непрерывным и, в отличие от распределения Пуассона, характеризуется двумя независимыми параметрами Х и 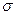. X - среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений. 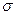- среднее стандартное отклонение (на интервал 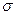[X- , X+ 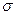] в среднем приходится 68%, а интервал 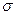[X-2 , X+2 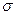] - 95% всех регистрируемых событий).

Оказывается, что если на результаты измерений оказывают влияние большое число источников небольших случайных ошибок, то вся совокупность измерений имеет в качестве предельного распределения симметричную колоколообразную функцию Гаусса. Центр распределения X, совпадающий с его максимумом, будет истинным значением измеряемой величины.

Распределение Гаусса (4.23) нормировано на единицу.

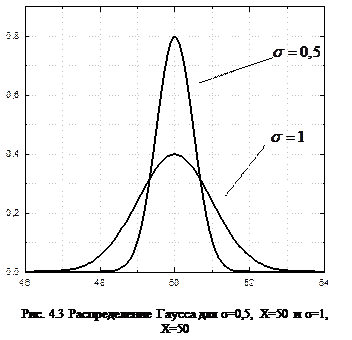
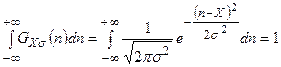.На рис. 4.3 показано два нормальных или гауссовых распределения, соответствующие различным измерениям с одинаковыми значениями X и разными s. В первом случае Х=50, 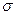=0,5, во втором случае - Х=50, 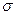=1. Величина 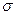в знаменателе экспоненты обеспечивает для более узкого распределения большую высоту в максимуме.

В случае распределения Гаусса ожидаемое среднее значение 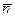для большого числа измерений можно вычислить по стандартной формуле

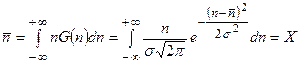. (4.24)

Этот результат почти очевиден, т. к. при большом числе измерений вследствие симметрии функции Гаусса одинаковое число результатов измерений окажется как больше X, так и меньше X. Среднее стандартное отклонение 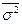определяется соотношением

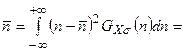
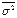. (4.25)

Сравним распределения Гаусса 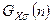и Пуассона .

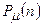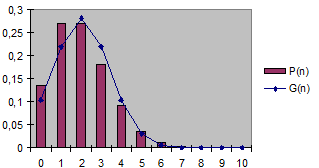
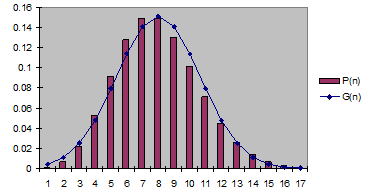
Рис. 4.4. Сравнение распределений Пуассона и Гаусса

1. Распределение Гаусса 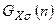является непрерывным, т.к. величина n может быть непрерывной, в то время как в распределении Пуассона 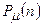величина n = 0, 1, 2, 3, … дискретна.

2. Распределение Гаусса определяется двумя параметрами: X - средней величиной и шириной распределения - стандартным отклонением 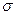, в то время как распределение Пуассона определяется единственным параметром 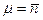, т.к. ширина распределения Пуассона 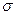автоматически определяется величиной ().

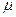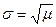3. При увеличении среднего числа отсчетов дискретная природа величины 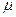в распределении Пуассона становится менее существенна, и распределение Пуассона хорошо аппроксимируется функцией Гаусса:

,

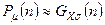при , .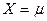

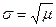На рис. 4.4 сравниваются распределение Пуассона и распределение Гаусса для двух значени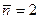й и 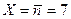. . 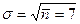Видно, что уже при достаточно малых значениях 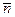распределения Пуассона и Гаусса практически совпадают. Необходимо иметь в виду, что распределения Пуассона и Гаусса совпадают только тогда, когда для распределения Гаусса 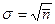. В общем случае распределение Гаусса характеризуется двумя независимыми параметрам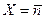и и 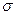. Величина 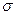может быть как больше 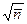, так и меньше.

В качестве примера распределения Гаусса укажем измерение энергетических спектров частиц. При измерении энергетических спектров заряженных частиц на выходе усилителя спектрометра мы имеем сигналы, амплитуда которых несет информацию об их энергиях. За счет различных процессов, носящих случайный характер (шумы детектора, флуктуации зарядового состояния ионов и т.п.), амплитуды сигналов от монохроматического источника имеют гауссово распределение, которое определяется двумя параметрами средним значением амплитуды сигнала Х и среднеквадратичным отклонением 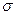. Разрешение спектрометра – это полная ширина на половине высоты (Full Width at Half Maximum - FWHM). В данном случае величины Х и 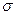в отличие от распределения Пуассона независимы