Итерационный метод решения разностной схемы

Пусть 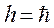. Тогда из (3) имеем

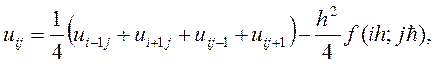
Определим алгоритм итерационного метода формулой

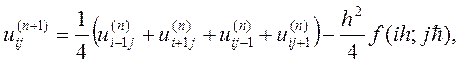
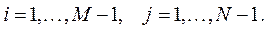
Для любого 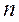остальные значения 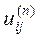в граничных узлах сетки определяются граничными условиями:

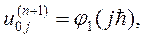
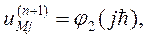
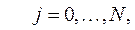
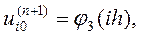
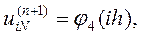
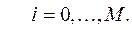
В качестве начального приближения выберем сеточную функцию :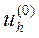

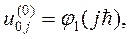
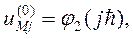
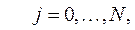
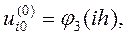
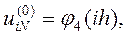
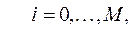
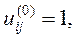
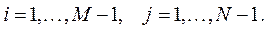
Покажем, что 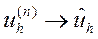при .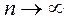

Обозначим, через 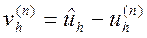ошибку 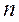-ого приближения. Тогда

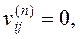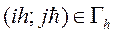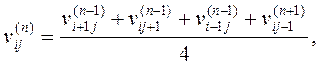если ,

если .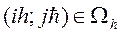

Положим 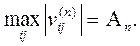Нужно доказать, что 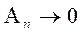при .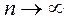

Имеет место неравенство

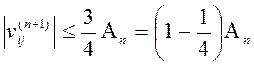для ,

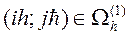где 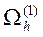- множество внутренних узлов сетки, находящихся на расстоянии равном 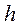от множества граничных узлов 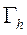, так как, по крайней мере, одно из слагаемых формулы (5) равно нулю. Далее получаем, что

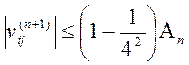для ,

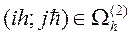где 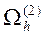- множество внутренних узлов сетки, находящихся на расстоянии равном 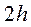от множества граничных узлов 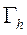, так как, по крайней мере, одно из слагаемых формулы (5) удовлетворяет предыдущему неравенству. Таким образом,

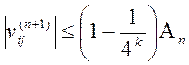для ,

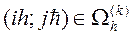где 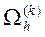- множество внутренних узлов сетки, находящихся на расстоянии равном 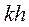от множества граничных узлов 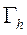, для любого 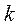, , 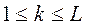здесь 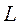- наибольшее расстояние от внутреннего узла сетки до множества ее граничных узлов.

Отсюда получаем, что 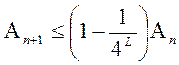и, следовательно, 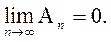Сходимость алгоритма доказана.