Общие сведения. Сортировка – это операция, упорядочивающая последовательность (массив) элементов по ключам

Сортировка – это операция, упорядочивающая последовательность (массив) элементов по ключам. Ключ – это некоторое числовое свойство элемента массива. Т. е. каждому элементу массива ставится в соответствие некоторое число, называемое ключом элемента.

Если мы имеем числовой массив, то ключ элемента – это сам элемент. В этом случае сортировка массива – это упорядочивание массива (перестановка его элементов) таким образом, чтобы получилась неубывающая или невозрастающая последовательность.

Если каждый элемент исходного массива представляет собой слова, составленные из букв русского алфавита, то ключ, по которому может быть упорядочен массив, связывается с порядковым номером буквы в алфавите. По этому принципу упорядочиваются слова в словарях – из двух слов первым помещается то слово, ключ которого меньше. Здесь принимается, что отсутствие буквы (т. е. пустая строка) имеет меньший ключ, чем любая другая буква. Так слово "студент" помещается в словаре перед словом "студентка".

Если слова состоят из букв разных алфавитов и цифр, как, например, имена файлов и папок, то любая цифра имеет меньший ключ, чем любая буква, а любая латинская буква имеет меньший ключ по сравнению с любой русской буквой. При сортировке таких имен в качестве ключа используется код символа в некоторой кодовой таблице. По этому принципу, например, отсортированы имена встроенных функций MS Excel в категории "Полный алфавитный перечень". Этот принцип упорядочивания еще называют лексикографическим порядком или расширенным алфавитом.

Разработкой различных алгоритмов сортировки информации, хранящейся в оперативной памяти компьютера или на его жестком диске, программисты занимаются уже давно. Интерес к этой проблеме обусловлен тем, что по мнению специалистов 25% всего времени обработки информации расходуется на сортировку данных.

Ясно, что с отсортированными данными работать легче, чем с произвольно расположенными. Когда элементы отсортированы, то проще найти нужный элемент или установить, что его нет.

Уточним терминологию.

Если элементы массива связаны отношениями 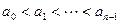, то говорят, что массив упорядочен по возрастанию. Такая упорядоченность предполагает, что в массиве нет одинаковых элементов.

Если элементы массива связаны отношениями 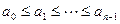, то говорят, что массив упорядочен по неубыванию. Такая упорядоченность не исключает наличие в массиве одинаковых элементов.

Если элементы массива связаны отношениями 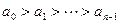, то говорят, что массив упорядочен по убыванию. Такая упорядоченность предполагает, что в массиве нет одинаковых элементов.

Если элементы массива связаны отношениями 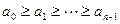, то говорят, что массив упорядочен по невозрастанию. Такая упорядоченность не исключает наличие в массиве одинаковых элементов.

Классификация методов сортировки

Все методы сортировки можно разделить на пять групп:

1) методы извлечения;

2) методы включения;

3) методы обменов;

4) методы слияния;

5) методы распределения.

Общая концепция методов извлечения заключается в следующем: из исходного массива извлекается минимальный элемент и меняется местами с первым элементом массива, затем извлекается минимальный элемент из части массива, начиная со второго элемента, и меняется местами со вторым элементом и т. д. Последний раз минимальный элемент выбирается из двух последних элементов массива. В результате получится массив, упорядоченный по неубыванию.

Различные методы извлечения отличаются объектом извлечения (минимальный или максимальный элемент) и, соответственно, объектами перестановки (первый или последний элемент), а также условием окончания процесса сортировки.

Алгоритм сортировки методом извлечения

Упорядочим заданный целочисленный массив по неубыванию на основе алгоритма извлечения минимального элемента.

Разработаем алгоритм сортировки на основе извлечения минимального элемента. Сначала запишем необходимые действия в словесной форме:

1) найдем минимальный элемент среди всех элементов массива 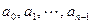и определим его номер. Пусть это будет элемент ;

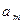2) поменяем местами элементы 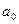и 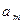. Таким образом, минимальный элемент массива окажется на своем окончательном месте;

3) теперь найдем минимальный элемент среди элементов массива, начиная со второго 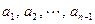и определим его номер. Опять обозначим этот элемент ;

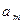4) поменяем местами элементы 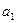и 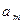. В результате два первых элемента массива окажутся на своих окончательных местах;

5) на заключительном этапе этого процесса надо выбрать минимальный элемент из двух последних элементов массива 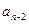и 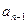. После чего этот элемент должен быть поставлен на предпоследнее место.

Теперь обобщим представленные шаги алгоритма следующим образом: нахождение минимального элемента 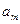среди элементов 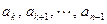и последующая перестановка элементов 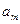и 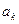, при этом указанный процесс должен повторяться при изменении k от 0 до n-2.

Идея методов включения состоит в том, что сначала первый элемент массива рассматривается как упорядоченный массив и в этот массив включается следующий элемент исходного массива так, чтобы получился упорядоченный по неубыванию массив из двух элементов. Затем в полученный упорядоченный массив включается третий элемент массива так, чтобы опять-таки получился упорядоченный массив. Процесс продолжается до тех пор, пока не будет включен последний элемент.

Различные алгоритмы включения отличаются способами выбора элемента для включения, способами определения места включения и методами самого включения.

Идея методов обменов состоит в следующем: в исходном массиве выбирается пара элементов, и они сравниваются между собой. Если их положение не удовлетворяет требованию упорядоченности, то элементы переставляются. Затем выбирается следующая пара элементов и так до тех пор, пока не получим упорядоченный массив.

Различные алгоритмы обменов отличаются способами выбора пары элементов для сравнения и перестановки, а также условиями окончания процесса сортировки.

Алгоритм сортировки методом обменов

Упорядочим заданный целочисленный массив по неубыванию на основе алгоритма " пузырька ", относящегося к алгоритмам обменов.

Сначала запишем необходимые действия в словесной форме:

1) сравним элементы 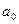и 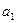. Если не выполняется условие, 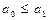,то меняем местами эти элементы и сравниваем элементы 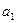и 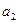. Так сравниваем и при необходимости меняем местами все пары исходного массива. Последней рассматривается пара 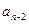и 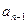. Так заканчивается первый просмотр массива, при котором максимальный элемент окажется на последнем месте. Это напоминает процесс вскипания воды: первым всплывает самый большой пузырек. Именно поэтому рассматриваемый способ сортировки называется методом "пузырька";

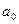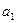2) второй просмотр массива опять-таки начинается со сравнения элементов и . Последней рассматривается пара 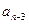и 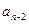. В результате на месте элемента 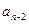окажется второй по величине элемент массива (всплыл второй по величине пузырек);

3) третий просмотр массива начинается с проверки пары 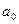и 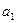, заканчивается проверкой пары 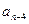и 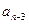, на месте элемента 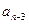окажется третий по величине элемент массива;

4) при последнем просмотре будут сравниваться только элементы 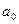и .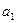

Теперь обобщим представленные шаги алгоритма следующим образом: просмотр массива состоит в проверке условия 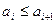и перестановке этих элементов при невыполнении условия неубывания, при этом значение переменной i изменяется от 0 до некоторого k, т. е. последнее проверяемое условие будет 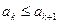. Первый просмотр происходит при k=n-2, следующий при k=n-3, затем при k=n-4 и т. д. до k=0.

Минимизация числа просмотров при сортировке методом "пузырька"

При сортировке методом "пузырька" часто встречается ситуация, когда массив уже отсортирован, а просмотры массива продолжаются. Чтобы вовремя прекратить процесс сортировки, будем фиксировать факт перестановки в какой-нибудь переменной.

Для этой цели лучше всего подходит переменная логического типа. Она принимает одно из двух значений: True или False.

С целью ускорения сортировки пузырьковым методом будем присваивать переменной W значение True всякий раз, когда после проверки очередной пары происходила перестановка значений сравниваемых элементов. Очередной оборот цикла для организации нового просмотра (цикл по переменной k) будем выполнять только в том случае, когда при предыдущем просмотре была сделана хотя бы одна перестановка. Перед началом цикла проверки упорядоченности (цикл по переменной i) надо переменной W присвоить значение False, признак того, что пока перестановок не было.

Сортировка методом обменов за один просмотр "с возвращением"

Рассмотрим еще один алгоритм сортировки методом обменов. Как и в алгоритме методом "пузырька", мы будем последовательно проверять на упорядоченность по неубыванию пары, начиная с 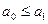и до 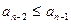. Однако после перестановки элементов, например 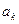и 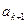, мы не будем сразу продолжать просмотр слева направо, а будем устанавливать правильное местоположение элемента 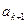, проверяя пары элементов справа налево. Таким образом, идея рассматриваемого алгоритма состоит в том, что после нахождения пары, не удовлетворяющей условию неубывания, т. е. пары 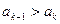, мы в упорядоченной части массива 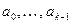отыскиваем такое место для элемента 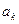, чтобы отсортированной оказалась часть массива 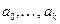. После этого можно продолжать просмотр массива слева направо, т. е. можно переходить к проверке условия .

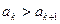В этом алгоритме внутренний цикл обеспечивает возврат от найденной неупорядоченной пары 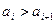к началу массива. Перед началом этого цикла переменной W присвоено значение True. Данный цикл заканчивается при выполнении одного из двух условий:

1) k=0 – проверены и переставлены все пары элементов, предшествующие элементу ;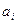

2) W=False – нашлась упорядоченная пара .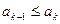

Метод слияния применяется в том случае, когда имеются два (или больше) упорядоченных массива и требуется соединить исходные массивы в один общий упорядоченный массив.

Алгоритм сортировки методом слияния

Рассмотрим алгоритм создания упорядоченного по неубыванию массива методом слияния двух массивов, один из которых упорядочен по невозрастанию, а другой - по неубыванию.

Имеем массив А из n элементов и массив В из m элементов:

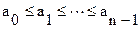, - неубывание;

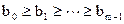- невозрастание.

Требуется получить массив с из n+m элементов:

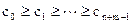- неубывание.

План решения задачи.

Пусть i - номер очередного элемента массива С. Тогда i=0,1,2,…,n+m-1.

Пусть k - номер максимального элемента среди оставшихся в массиве А. Сначала k=n-1. По мере переписывания элементов из массива А в массив С k уменьшается на единицу (k=k-1).

Пусть l - номер максимального элемента среди оставшихся в массиве B. Сначала l=0. По мере переписывания элементов из массива B в массив С l увеличивается на единицу (l = l +1).

Если не исчерпаны элементы в массивах A и B, то 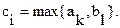Если же исчерпаны элементы в массиве A, то 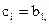, затем l = l +1. Если же исчерпаны элементы в массиве B, то 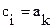, затем k=k-1.

Метод распределения употребим в тех случаях, когда в исходном массиве имеется заданное, известное заранее, количество различных ключей (значений). Например, имеется список студентов с оценками по пятибалльной системе, полученными на экзамене. Нам известно заранее, что оценки могут быть 5, 4, 3 и 2. Поэтому для упорядочения массива по невозрастанию можно сначала выбрать все записи с оценками 5, затем с оценками 4, потом с оценками 3 и, наконец, с оценками 2.

Использование встроенной функции qsort из библиотеки stdlib для сортировки массива записей

Дан массив записей, состоящий из полей: имя, фамилия, год рождения. Вывести в алфавитном порядке записи по полю фамилия, используя встроенную функцию сортировки qsort.

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

//Шаблон структуры студенты

typedef struct{

char name[20];

char family[20];

int year;

} TStudent;

//Как сравнить 2-х студентов по фамилии. Эта процедура будет являться параметром //функции сортировки

int sort_cmp(const void *a, const void *b)

{

TStudent *x = (TStudent *)a; //x - pointer to the first student

TStudent *y = (TStudent *)b; //y - pointer to the second

return(strcmp(x->family, y->family)); //compare by family

/*

Если хотите сравнить по году рождения

if(x->year < y->year) return -1;

else if(x->year == y->year) return 0;

else return 1;

*/

}

int main(void)

{

int i;

//Ввод данных

const int StudCount = 4;

TStudent students[StudCount] = {

{"Alexander", "Farberov", 1987},

{"Dmitry", "Hrabrov", 1988},

{"Denis", "Shulga", 1988},

{"Boris", "Abramovich", 2666}

};

//Сортировка

qsort((void *)students, StudCount, sizeof(TStudent), sort_cmp);

//Вывод

puts("The students are:");

for (i = 0; i < StudCount; i++)

printf("%d. %s %s %d\n", i+1,

students[i].family, students[i].name, students[i].year);

return 0;

}

qsort(a, n, sizeof(int), cmp);

Это функция, описанная в стандартной библиотеке ANSI C и объявлена в заголовочном файле stdlib.h.

Поэтому в начале программы нужно добавить

#include <stdlib.h>

Функцией qsort можно упорядочивать объекты любой природы. По сути, она предназначена упорядочивать множества блоков байтов равной длины. Второй аргумент функции — это число таких блоков, третий аргумент — длина каждого блока. Первый аргумент — это адрес, где находится начало первого блока (предполагается, что блоки в памяти расположены друг за другом подряд).

Четвёртый аргумент функции qsort — это имя функции, которая умеет сравнивать два элемента массива. В нашем случае это

int cmp(const void *a, const void *b) {

return *(int*)a - *(int*)b;

}

В силу указанной универсальности функции сортировки, функция сравнения получает в качества аргумента адреса двух блоков, которые нужно сравнить и возвращает 1, 0 или -1:

положительное значение, если a > b

0, если a == b

отрицательное значение, если a < b

Поскольку у нас блоки байт -- это целые числа (в 32-битной архитектуре это четырёхбайтовые блоки), то необходимо привести данные указатели типа (const void*) к типу (int *) и осуществляется это с помощью дописывания перед указателем выражения «(const int*)». Затем нужно получить значение переменной типа int, которая лежит по этому адресу. Это делается с помощью дописывания спереди звездочки.

Таким образом, мы получили следующую программу

#include <stdio.h>

#include <stdlib.h>

#define N 1000

int cmp(const void *a, const void *b) {

return *(int*)a - *(int*)b;

}

int main() {

int n, i,j;

int a[N];

scanf("%d", &n);

for(i = 0; i < n; i++) { // ЧИТАЕМ ВХОД

scanf("%d", &a[i]);

}

qsort(a, n, sizeof(int), cmp); // СОРТИРУЕМ

for(i = 0; i < n; i++) { // ВЫВОДИМ РЕЗУЛЬТАТ

printf("%d ", a[i]);

}

return 0;

}

Динамическое выделение памяти[править]

Ниже приведена программа, где память под массив выделяется динамически:

#include <stdio.h>

#include <stdlib.h>

#include <malloc.h>

#define N 1000

int cmp(const void *a, const void *b) {

return *(int*)a - *(int*)b;

}

int main() {

int n, i;

int *a;

scanf("%d", &n);

a = (int*) malloc(sizeof(int)*n);

for(i = 0; i < n; i++) {

scanf("%d", &a[i]);

}

qsort(a, n, sizeof(int), cmp);

for(i = 0; i < n; i++) {

printf("%d ", a[i]);

}

free(a);

return 0;

}

Обратите внимание на сложное приведение типов.

Функция strcmp, объявленная в файле string.h имеет следующий прототип:

int strcmp(const char*, const char*);

То есть функция получает два аргумента -- указатели на кусочки памяти, где хранятся элементы типа char, то есть два массива символов, которые не могут быть изменены внутри функции strcmp (запрет на изменение задается с помощью модификатора const).

В то же время в качестве четвертого элемента функция qsort хотела бы иметь функцию типа

int cmp(const void*, const void*);

В языке Си можно осуществлять приведение типов являющихся типами функции. В данном примере тип

int (*)(const char*, const char*); // функция, получающая два элемента типа 'const char *' и возвращающая элемент типа 'int'

приводится к типу

int (*)(const void*, const void*); // функция, получающая два элемента типа 'const void *' и возвращающая элемент типа 'int'

Функция strcmp в соответствии с описанием, осуществляет сравнение двух строк и определяет, какая из двух строк идёт первой в алфавитном порядке (сравнивает две строки в лексикографическом порядке), а именно: она возвращает 1, если первая строка "больше" второй (идёт после второй в алфавитном порядке), 0 – если они совпадают, и -1 – если первая строка "меньше" второй.