Как и для систем алгебраических уравнений одним из методов решения является метод исключения. С его помощью решение системы сводится к решению одного дифференциального уравнения второго порядка. Поясним этот метод на примере решения системы линейных однородных уравнений с постоянными коэффициентами.
Пример 12. Найти общее решение системы дифференциальных уравнений
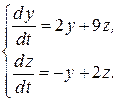
Исключим из первого уравнения неизвестную функцию z. Для этого сначала продифференцируем его по t.
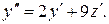
Затем подставим 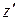 из второго уравнения
из второго уравнения
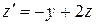 ,
,
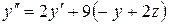 ,
,
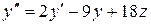 . (1)
. (1)
Выразим 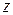 из первого уравнения
из первого уравнения
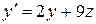 ,
,
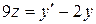 ,
,
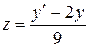 . (2)
. (2)
Подставим полученное выражение для 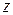 в (1)
в (1)
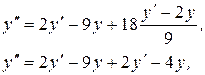
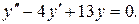 (3)
(3)
Получили линейное дифференциальное уравнение второго порядка. Корни характеристического уравнения 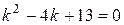 равны
равны
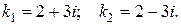
Тогда общее решение (3) имеет вид
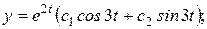
Чтобы найти 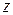 , подставим в (2) выражения для
, подставим в (2) выражения для 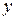 и
и 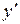 .
.
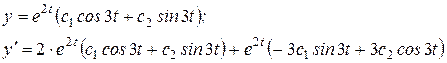
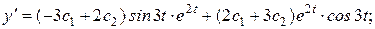
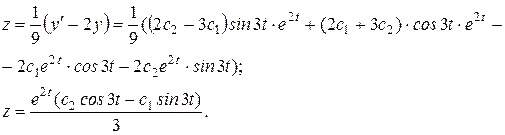
Итак, получили общее решение системы
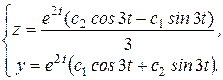
ВОПРОСЫ И УПРАЖНЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Дайте определения дифференциального уравнения, его общего и частного решений. Сформулируйте задачу Коши для уравнения первого порядка и укажите его геометрический смысл.
2. Изложите метод решения уравнений с разделенными и разделяющимися переменными.
3. Сформулируйте определение линейного уравнения первого порядка. Изложите метод подстановки для нахождения его общего решения.
4. Как интегрируются уравнения вида F(x, y¢, y¢¢)=0, F(y, y¢, y¢¢)=0?
5. Какой общий вид имеет линейное уравнение второго порядка (однородное и неоднородное)? Какие решения его называются линейно-независимыми? Как получить общее решение однородного линейного уравнения с постоянными коэффициентами?
6. Найти общие решения дифференциальных уравнений:
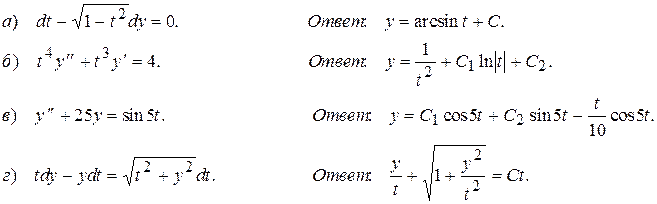 д)
д) 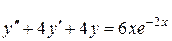 . Ответ:
. Ответ: 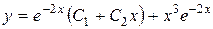 .
.
е) 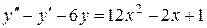 . Ответ:
. Ответ: 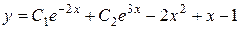 .
.
7. Решить задачу Коши:
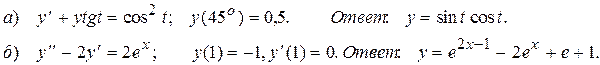
8. Решить системы уравнений:
а) 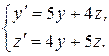 Ответ:
Ответ: 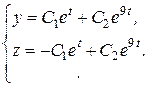
б) 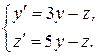 Ответ:
Ответ: 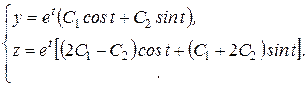
КОНТРОЛЬНАЯ РАБОТА №3
 Указать тип дифференциальных уравнений и найти их решение. Там, где даны начальные условия, кроме общего, найти соответствующее частное решение.
Указать тип дифференциальных уравнений и найти их решение. Там, где даны начальные условия, кроме общего, найти соответствующее частное решение.
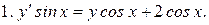
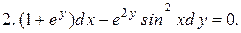
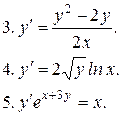
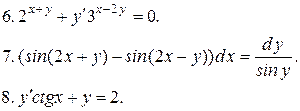
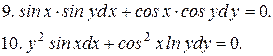
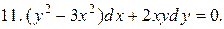
12. 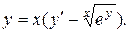
13. 
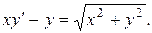
14. 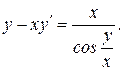
15. 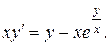
16. 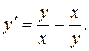
17. 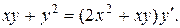
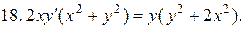
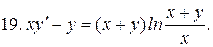
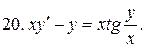
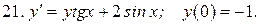
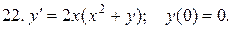
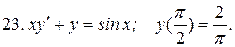
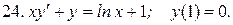
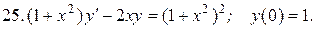
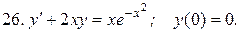
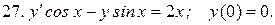
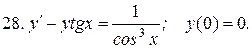
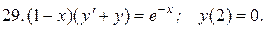
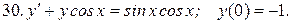
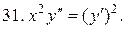
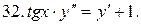
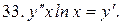
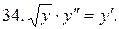
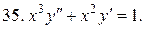
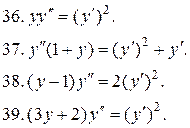
40. 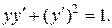
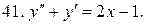
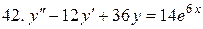
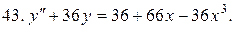
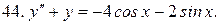
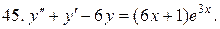
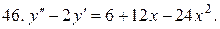
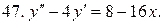
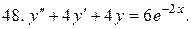
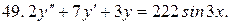
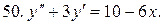
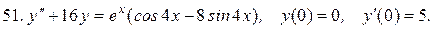
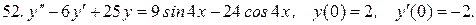
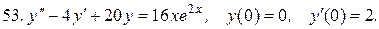
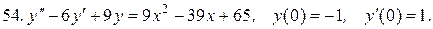
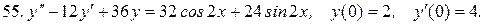
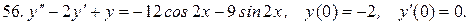
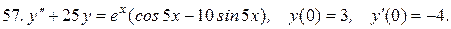
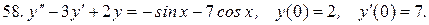
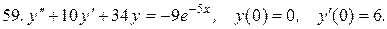
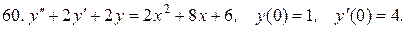
Решить системы дифференциальных уравнений.
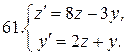
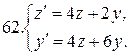
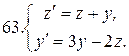
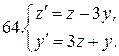
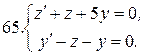
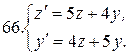
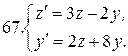
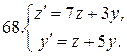
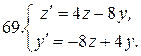
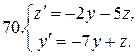
 2015-06-05
2015-06-05 705
705








