I. Линейное однородное дифференциальное уравнение с постоянными коэффициентами имеет вид
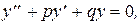 (11)
(11)
где p и q -действительные числа.
Чтобы решить данное уравнение, надо составить и решить характеристическое уравнение
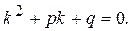 (12)
(12)
Если корни характеристического уравнения действительны и различны, 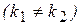 , то общее решение уравнения (11) выражается формулой
, то общее решение уравнения (11) выражается формулой
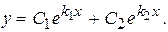 (13)
(13)
Если же корни действительны и одинаковы 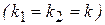 , то общее решение имеет вид
, то общее решение имеет вид
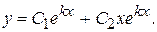 (14)
(14)
Наконец, в случае комплексных корней 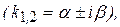 общее решение имеет вид
общее решение имеет вид
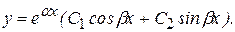 (15)
(15)
Пример 8. Решить уравнение
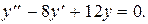
Решение. Составляем и решаем характеристическое уравнение
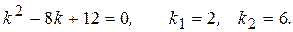
Так как корни квадратного уравнения являются действительными и разными, общее решение имеет вид
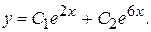
Пример 9. Найти частное решение уравнения
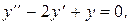
удовлетворяющее заданным условиям 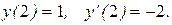
Решение. Характеристическое уравнение 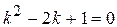 имеет корни
имеет корни 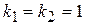 . Поэтому общее решение имеет вид
. Поэтому общее решение имеет вид
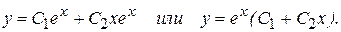
Для нахождения частного решения продифференцируем y.
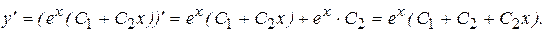
Подставив выражения для y и y¢ в начальные условия, получим систему линейных алгебраических уравнений относительно С 1 и С2 .
|
|
|
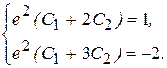
Решив ее, найдем 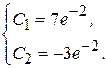
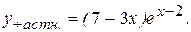
Пример 10. Напряжение в электрической цепи во время переходного процесса описывается уравнением
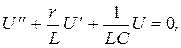
где r, L, C - постоянные величины, характеризующие сопротивление, индуктивность и емкость цепи. Найти функцию U(t), если 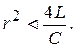
Решение. Характеристическое уравнение
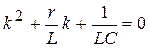
имеет комплексные корни 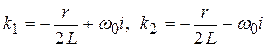 (
(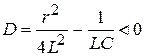 ), где
), где 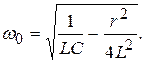 В общем случае решение имеет вид
В общем случае решение имеет вид
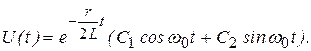
Преобразуем его, приняв 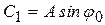 и
и 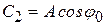 . Тогда
. Тогда
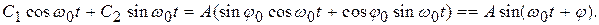
Отсюда
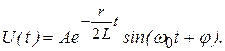
Последняя формула описывает затухающие синусоидальные колебания с частотой 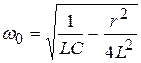 и амплитудой
и амплитудой 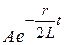 , уменьшающейся с течением времени.
, уменьшающейся с течением времени.
II. Общее решение линейного неоднородного уравнения с постоянными коэффициентами
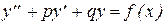
равно сумме общего решения y0.0. соответствующего однородного уравнения 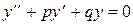 и какого-нибудь частного решения исходного неоднородного уравнения yч.н.
и какого-нибудь частного решения исходного неоднородного уравнения yч.н.
y=y0.0.+ yч.н.
.
Если правая часть уравнения состоит из сумм и произведений функций 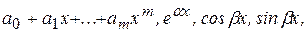 частное решение можно искать методом подбора или методом неопределенных коэффициентов. Для перечисленных функций частное решение неоднородного уравнения имеет сходный с правой частью уравнения вид (см. таблицу 1).
частное решение можно искать методом подбора или методом неопределенных коэффициентов. Для перечисленных функций частное решение неоднородного уравнения имеет сходный с правой частью уравнения вид (см. таблицу 1).
Таблица 1.
Структура частного решения линейного неоднородного
дифференциального уравнения с постоянными коэффициентами
в зависимости от вида правой части уравнения
| Вид правой части уравнения | Корни характеристического уравнения | Вид частного решения |
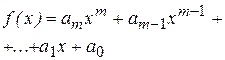 | a=0, b=0, a+ib=0, k¹0 k=0 | yч.н.= 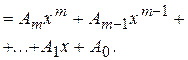 yч.н = yч.н = 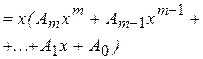 |
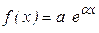 | b=0, a+ib=a, k1¹a и k2¹a a= k1 или a= k2 k1=k2=a | yч.н. 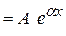 yч.н. yч.н. 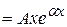 yч.н. yч.н. 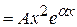 |
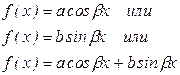 | a=0, a+ib= i b, k1¹ i b и k2¹ i b k1= i b или k2= i b | yч.н. 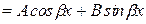 yч.н. = yч.н. = 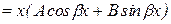 |
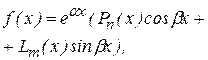 где Рn(x) -многочлен n-ой степени, Lm(x)- многочлен m-ой степени от x где Рn(x) -многочлен n-ой степени, Lm(x)- многочлен m-ой степени от x  | 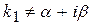 и и 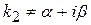 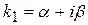 или или 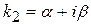 | yч.н. = 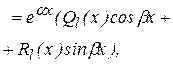 где l - наибольшее из чисел m и n, yч.н. = где l - наибольшее из чисел m и n, yч.н. = 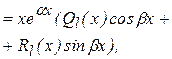 |
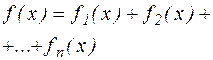 | yч.н 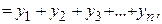 где yi - частное решение уравнения с той же левой частью и правой частью, равной fi(x) (i=1,2,...n). где yi - частное решение уравнения с той же левой частью и правой частью, равной fi(x) (i=1,2,...n). |
Неопределенные коэффициенты А0,А1,...,Аm,А,В,...определяют следующим образом: находят производные и подставляют yч.н. y¢ч.н., и y¢¢ч.н. в левую часть уравнения. Затем, приравнивая коэффициенты при одинаковых степенях независимой переменной и синусах и косинусах в левой и правой частях дифференциального уравнения, составляют систему алгебраических уравнений для нахождения значений неопределенных коэффициентов.
|
|
|
Пример 11. Решить уравнение 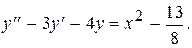
Решение. Заданное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Соответствующее однородное уравнение -
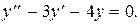
Его характеристическое уравнение 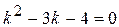 имеет корни k1=4, k2=-1.
имеет корни k1=4, k2=-1.
Отсюда
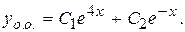
Теперь найдем частное решение данного неоднородного уравнения. Так как правая часть не содержит множителей 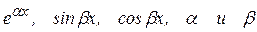 полагаем равными нулю (
полагаем равными нулю (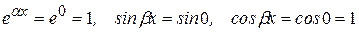 ). Тогда a+ ib=0, 0 не является корнем характеристического уравнения. Правая часть уравнения представляет собой многочлен второй степени (хотя и неполный), поэтому решение будем искать в виде
). Тогда a+ ib=0, 0 не является корнем характеристического уравнения. Правая часть уравнения представляет собой многочлен второй степени (хотя и неполный), поэтому решение будем искать в виде
yч.н.=А2 x 2+A1 x +A0.
Находим производные и подставляем в данное уравнение:
y¢ч.н.=2А2 x +A1.
y¢¢ч.н.=2А2,
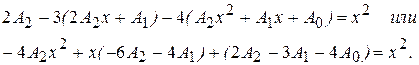
Чтобы последнее равенство стало тождеством, приравниваем коэффициенты при одинаковых степенях x.
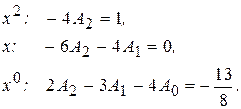
 Решив систему, найдем
Решив систему, найдем
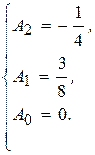
Таким образом, частное решение неоднородного уравнения
yч.н. 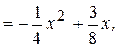
а общее решение имеет вид
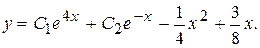
 2015-06-05
2015-06-05 1034
1034








