2015-06-05
454
1. Уравнения с разделенными переменными имеют вид
f2(y)dy=f1(x)dx, (4)
или
f2(y)dy+f1(x)dx=0 (5)
Считая функцию y известной функцией от x, равенство (4) можно рассматривать как равенство двух дифференциалов. Тогда неопределенные интегралы от них будут отличаться постоянным слагаемым. Проинтегрировав левую часть по y, а правую по x, получим общий интеграл уравнения (4).
.
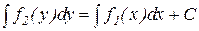Уравнение (5) также интегрируется непосредственно
.
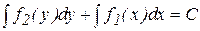Частным случаем уравнения (4) является уравнение y'=f(x), не содержащее неизвестной функции y=y(x) или,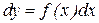 
, общее решение которого 
.
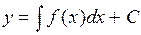2. Если дифференциальное уравнение можно привести к виду (4), то оно называется уравнением с разделяющимися переменными.
Пример 1. Найти общее решение уравнения y'=ex+y.
Решение. Запишем уравнение в виде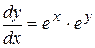 
, 
, 
, 
, 
, 
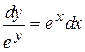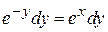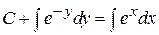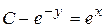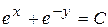- общий интеграл дифференциального уравнения.
Пример 2. Найти общее решение уравнения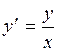 
.
Решение.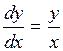 
. Разделяем переменные, умножив обе части уравнения на dx и разделив на y: 
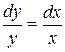. Интегрируем: 
, 
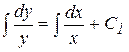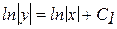. Чтобы получить решение в более простой форме, С1 заменим на lnïCï, C¹0, так как любое число С1 может быть представлено в виде натурального логарифма другого положительного числа ïСï. Тогда 
. 
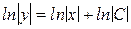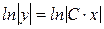, откуда y=Cx.
Замечание. Разделив обе части на y, мы могли потерять решение y=0. Действительно, y=0 - решение исходного уравнения, так как подставив в него y=0, получим тождество 0=0. Это частное решение можно получить из общего при С=0. Таким образом, общее решение имеет вид y=Cx,где С - любое действительное число (в том числе и 0).
3. Уравнение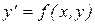 
называется однородным, если функция f(x,y) удовлетворяет условию
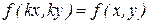. (6)
Функцию, удовлетворяющую этому условию, можно представить в виде
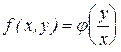. (7)
Путем введения новой неизвестной функции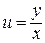 
однородное уравнение 
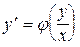приводится к уравнению с разделяющимися переменными. Действительно,
, 
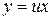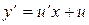.. (8)
Подставив выражения для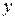 
и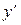 
в уравнение (7), получим
,
,
.
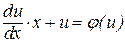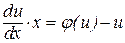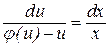После того как уравнение будет проинтегрировано, следует u заменить на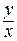 
.
Пример 3. Найти общее решение уравнения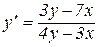 
.
Решение. В том, что это однородное уравнение легко убедиться, заменив x на kx, а y на ky.
.
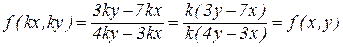Используя формулы (8), приведем уравнение к виду
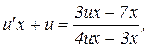
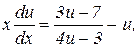
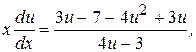
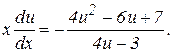
Разделяем переменные:
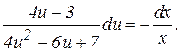
Интегрируя, получим
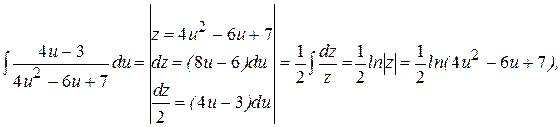
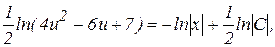
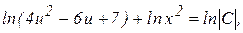
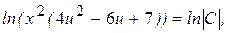
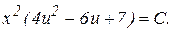
Заменив u на y/x, получим общий интеграл уравненияв виде
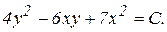
4. Линейным называется дифференциальное уравнение, линейное относительно искомой функции и ее производной. Его стандартный вид
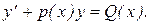(9)
Функции p(x) и Q(x) предполагаются непрерывными в той области, в которой ищется решение уравнения (9).
Один из способов решения линейных уравнений первого порядка состоит в следующем. Искомую функцию представляют в виде произведения двух неизвестных функций, одну из которых подбирают так, чтобы уравнение упростилось. Пусть y=uv. Тогда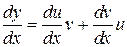 
и уравнение примет вид
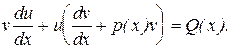(10)
Функцию n подбирают так, чтобы выражение в скобках обращалось в нуль, т.е.
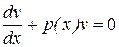
и ищут частное решение v=v(x) этого уравнения с разделяющимися переменными, приняв постоянную интегрирования равной нулю.
Подставим найденное решение в уравнение (10). Так как выражение в скобках равно нулю, то оно сводится к уравнению с разделяющимися переменными
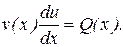
Найдя его общее решение в виде u=u(x,C), получим общее решение уравнения (9)
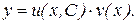
Пример 4. Найти общее решение уравнения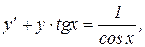 
Решение.
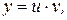
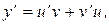
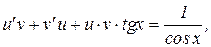
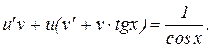
Выражение в скобках приравниваем к нулю. Тогда линейное уравнение распадается на два уравнения с разделяющимися переменными
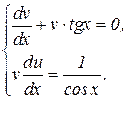
Из первого уравнения найдем v.
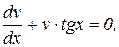
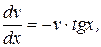
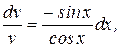
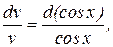
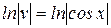(выбираем С =0),
.
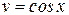Тогда второе уравнение примет вид
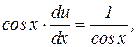
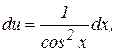
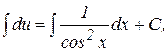
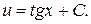
Общее решение исходного уравнения
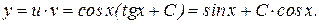
Пример 5. Найти закон установления тока при замыкании цепи с сопротивлением r, индуктивностью L и э.д.с. источника e.
Решение. По второму правилу Кирхгофа
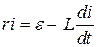или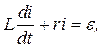 
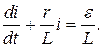
Данное уравнение является линейным относительно искомой функции i(t), характеризующей силу тока в цепи в момент времени t. Требуется найти частное решение, удовлетворяющему условию: при t=0 i=0.
Полагаем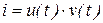 
. Тогда
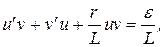
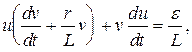
Приравниваем выражение в скобках к нулю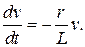 
Разделяя переменные и интегрируя, получим
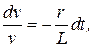
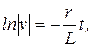
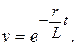
Подставив выражение для v в уравнение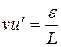 
, определим u
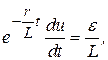
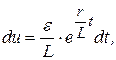
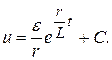
Общее решение исходного уравнения
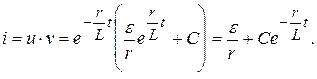
Подставив в него начальное условие (i=0; t=0), найдем С:
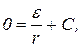
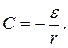
Следовательно, искомое частное решение имеет вид
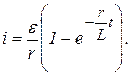
Анализ полученного решения показывает, что
1) с ростом t вследствие быстрого убывания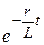 
вторым слагаемым можно пренебречь и сила тока будет подчиняться закону Ома;
2) при увеличении индуктивности L процесс установления тока замедляется, что объясняется законом Ленца: экстратоки самоиндукции препятствуют изменениям тока, их вызвавшим.
