Дифференциальные уравнения

К сдаче экзамена или зачета допускаются студенты, имеющие на руках зачтенные контрольные работы.

Таблица 1

Варианты контрольных заданий

№ варианта	№№ задач

РАБОЧАЯ ПРОГРАММА

Дифференциальные уравнения.

1. Основные определения: порядок уравнения, общее и частное решения, задача Коши.

2. Уравнения с разделяющимися переменными.

3. Однородные дифференциальные уравнения первого порядка.

4. Линейные дифференциальные уравнения первого порядка.

5. Дифференциальные уравнения второго и высших порядков. Способы понижения порядка дифференциальных уравнений.

6. Однородные линейные дифференциальные уравнения второго порядка. Фундаментальная система решений и общее решение.

7. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение.

8. Структура общего решения неоднородного линейного дифференциального уравнения.

9. Неоднородные линейные уравнения с постоянными коэффициентами и правой частью специального вида. Метод неопределенных коэффициентов (метод подбора).

10. Системы линейных однородных уравнений первого порядка с постоянными коэффициентами.

ЛИТЕРАТУРА

1. Пискунов Н.С. Дифференциальное и интегральное исчисление. т.2.- М.: Наука, 1976 (и последующие издания).

2. Романовский П.И. Ряды Фурье. Теория Паскаля. Аналитические и специальные функции. Преобразования Лапласа. М.: «Наука», 1979.

3. Колобов А.М. Избранные главы высшей математики. Мн.: Высшая школа. 1965.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1989.

5. Гусак А.А. Пособие к решению задач по высшей математике. - Мн.: Вышэйшая школа, 1967.

6. Руководство к решению задач по высшей математике. /Под ред. Гурского Е.И. Часть I. - Мн.: Вышэйшая школа, 1989.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Уравнения, в которые неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями.

Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называется обыкновенным. Если уравнение содержит неизвестную функцию двух или большего числа независимых переменных, то оно называется уравнением в частных производных.

Порядком дифференциального уравнения называется порядок наивысшей производной неизвестной функции, входящей в уравнение. Дифференциальное уравнение первого порядка имеет вид

F(x,y,y')=0, (1)

порядка n -

F(x,y,y',y'',...,y⁽ⁿ⁾)=0. (2)

Частным решением дифференциального уравнения называется функция y=y(x), которая обращает это уравнение в тождество.

Множество всех частных решений называется общим решением дифференциального уравнения. Процесс нахождения решения называется интегрированием дифференциального уравнения.

Общее решение дифференциального уравнения первого порядка записывается в виде y=j(x,C), где С - произвольная постоянная, или Ф(x,y,C)=0, определяющему y как неявно заданную функцию от x и называемому общим интегралом дифференциального уравнения. Придавая С различные значения, получают частные решения дифференциального уравнения. На практике частное решение выделяют из общего, задавая дополнительное условие, которому должна удовлетворять искомая функция. Чаще всего такое условие включают в задачу, называемую задачей Коши: найти решение y=j(x) дифференциального уравнения F(x,y,y')=0, которое при заданном значении x₀ принимает заданное значение y₀. Это условие y=y₀ при x= x₀ называется начальным. Оно часто записывается в виде .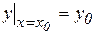

Общее решение дифференциального уравнения порядка выше первого зависит от стольких произвольных постоянных, каков порядок уравнения, т.е. общее решение дифференциального уравнения n -порядка y=j(x,C₁,C₂,...,C_n) зависит от n произвольных постоянных C₁,C₂,...,C_n, а задача Коши имеет вид

F(x,y,y',y'',...,y⁽ⁿ⁾)=0,

y(x₀)=y₀,

y'(x₀)=y₀', (3)

.......

y^(n-1)(x₀)=y₀^(n-1).