2015-06-05
377
Если дан ряд (1), то сумма первых n членов этого ряда называется n-ой частичной суммой и обозначается через An. Следовательно, суммы
A 1= a1 – 1-ая частичная сумма;
A 2= a1+a2 – 2-ая частичная сумма;
A 3= a1+a2+a3 – 3-ая частичная сумма;
¼
A n= a1+a2+a3+ ¼+ an – n-ая частичная сумма,
...
образуют последовательность частичных сумм A 1, A 2,..., A n,....
Определение.
Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм, то есть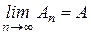 
. При этом число A называется суммой ряда. Если для данного ряда последовательность частичных сумм { A n} не имеет конечного предела при n ®¥, то этот ряд называется расходящимся.
Пример 13. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии (геометрический ряд)
a + aq + aq 2 +...+ aqn -1 +...=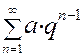 
( a ¹0).
Решение. Из элементарной математики известно, что сумма n членов геометрической прогрессии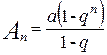 
. Отсюда следует, что если ï q ï<1, то геометрический ряд сходится и его сумма 
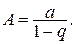Если же ï q ï³1, то геометрический ряд расходится.
|
|
|
Пример 14. Исследовать на сходимость ряд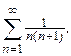 
Решение. Так как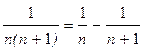 
, то n-ая частичная сумма данного ряда
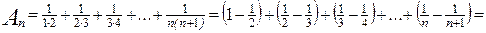
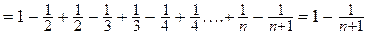. Эта сумма при n®¥ имеет предел 
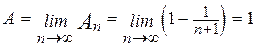. Итак, данный ряд сходится и его сумма равна единице.
