Знакочередующиеся ряды

Определение.

Числовой ряд называется знакочередующимся, если его члены поочередно меняют знак. Знакочередующийся ряд можно записать в виде

a ₁ - a ₂ + a ₃ - a₄ +...+ 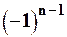a _n +...= 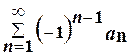, ( 19 )

где а _n>0.

Для знакочередующихся рядов имеет место следующий очень простой достаточный признак сходимости.

ТЕОРЕМА 7. (Признак Лейбница)

Если для знакочередующегося ряда (19) все его члены удовлетворяют условиям:

а) a ₁ > a ₂ > a ₃ > a₄ >...> a _n >... (т.е. члены ряда монотонно убывают по абсолютной величине);

б) 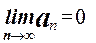(т.е. общий член ряда стремится к нулю при n®¥), то такой ряд сходится, а его сумма не превосходит первого члена.

Пример 24. Исследовать сходимость ряда .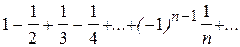

Решение. Данный знакочередующийся ряд сходится, так как удовлетворяет условиям признака Лейбница:

а) ;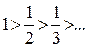

б) .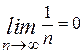

Заметим, что данный ряд отличается от гармонического только знаками четных членов.