2015-06-10
306
Для характеристики рассеивания возможных значений случайной величины вокруг математического ожидания используется математическое ожидание квадратов этих отклонений, т.е.
,
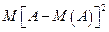называемое дисперсией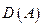 
. Поэтому свойства дисперсии определяются свойствами математического ожидания. Приведенная формула дисперсии допускает упрощение:
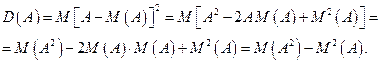
Здесь учтено, что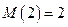 
, 
, 
.
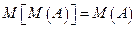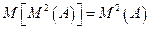Отметим, что дисперсия является неслучайной, (детерминированной, постоянной) величиной, характеризирующей случайную величину в целом (суммарно, интегрально).
