Математическое ожидание (центр распределения) числа отказов технической системы

Общей (суммарной, интегральной) числовой характеристикой случайной величины является взвешенное по вероятности среднее арифметическое значение, определяемое непосредственно по закону распределения (таблице, матрице) и называемое математическим ожиданием (центром распределения):

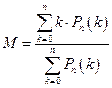
Здесь

.

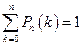Тогда

.

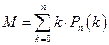Пример:

.

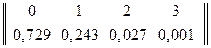
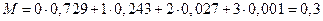Математическое ожидание биномиального распределения случайной

величины находится по определению:

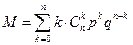
Проведем преобразования этой формулы, исходя из того, что

.

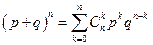Дифференцируем это равенство по переменной :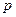

.

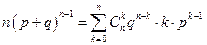Умножаем полученное равенство на переменную :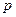

.

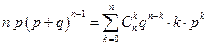Откуда

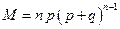
и так как 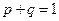, получим

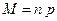
Математическое ожидание распределения Пуассона находится аналогично:

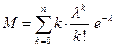
или

.

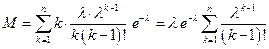Учитывая, что

,

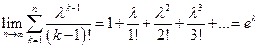получим

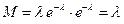
т.е.

.

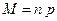Отметим, что математическое ожидание является неслучайной (детерминированной, постоянной) величиной, характеризующей случайную величину в целом (суммарно, интегрально).