Дисперсия числа отказов технической системы

В условиях предыдущего примера оценить рассеивание (дисперсию) случайной величины 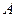− число отказов в TS за установленное время.

Очевидно, что

,

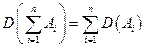где

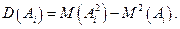
Так как 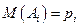и закон распределения 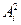имеет вид

,

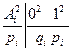
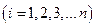то

.

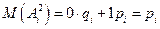Тогда

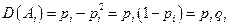
и искомая дисперсия определится по формуле

.

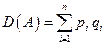В частности, для однородных элементов 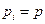и 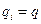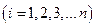, получим

.

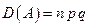Дисперсия биномиального распределения случайной величины находится в виде:

,

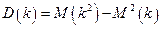где

,

.

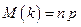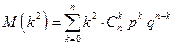Дважды дифференцируя по переменной 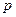очевидное равенство:

,

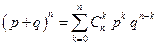получим

.

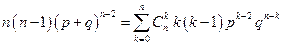Умножая это равенство на 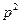, найдем

.

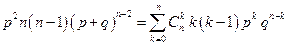Учитывая, что 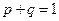, получим

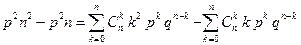
или

.

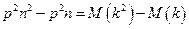Откуда

.

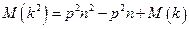Таким образом,

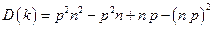
или

,

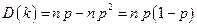т.е.

,

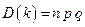что соответствует ранее установленному результату.

Дисперсия случайной величины, распределенной по закону Пуассона определяется аналогично:

,

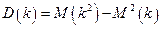где

,

.

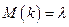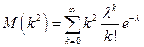Здесь

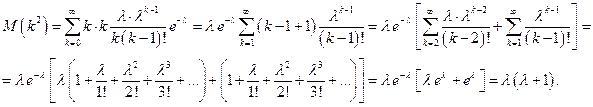
Таким образом,

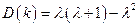
или

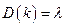, т.е. ,

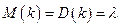что является характерным признаком распределения Пуассона.