Оптимизация выбора количественного состава оборудования
Постановка задачи
Одним из первых этапов в создании проекта участка гибкого производственного производства (ГАП) и, в частности, в проектировании его транспортной подсистемы, является решение задач выбора и размещения оборудования участка. Эти задачи являются сложными многопараметрическими и многокритериальными оптимизационными задачами.
Задачу выбора технологического состава оборудования можно разбить на две подзадачи: задачу выбора количественного состава оборудования и задачу выбора качественного состава. В первом случае необходимо при конкретном заданном наборе оборудования выбрать оптимальный количественный состав оборудования в каждой группе технологического оборудования, занятой в заданном технологическом процессе.
При выборе количественного состава оборудования исходными данными являются параметры технологического процесса, общее количество позиций обработки и типаж технологического оборудования. Задача выбора количественного состава ставится как задача определения количества единиц оборудования в группах, отвечающих позициям обработки. Эта задача рассматривается в двух дополняющих и последовательно расширяющих друг друга вариантах. На первом этапе количественный состав оборудования определяется из уравнений баланса межгруппового обмена продукцией с учетом времен обработки на позициях участка, заданных потоков обрабатываемых изделий между различными группами оборудования, требуемой производительности участка, заданных рабочих площадей и обобщенных стоимостей, выделяемых на оборудование и его установку.
На втором этапе вводятся ограничения на допустимый разбаланс оборудования в группах. Эти условия соответствуют ограничениям на взаимно обусловленные простои оборудования при рассогласовании требований различных потоков обрабатываемых изделий, например, при широкой номенклатуре изделий участка ГАП. А также рассматривается дополнительный критерий – время, необходимое на переналадку оборудования при переходе от одной модификации к другим.
Далее рассмотрим задачу выбора количественного состава оборудования для участка ГАП и математический аппарат, который используется для решения данной задачи.
Математическое обеспечение расчета количественного состава оборудования
Пусть на рассматриваемом участке намечен выпуск продукции L модификаций и для каждого 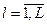 задано Г l – количество изделий l –ой модификации, которое необходимо выпускать на данном участке в единицу времени.
задано Г l – количество изделий l –ой модификации, которое необходимо выпускать на данном участке в единицу времени.
Пусть для каждой из модификаций известен ее технологический маршрут (последовательность операций, необходимых для производства продукции данной модификации).
Будем рассматривать технологические маршруты двух типов: технологические маршруты типа «механообработки» и маршруты типа «механосборки».
Маршруты задаются либо в виде графов, как, например, показано на рисунке 1.3.1, либо с помощью матриц технологических маршрутов C l, 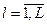 , размерности N
, размерности N 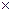 N, где N – число различных групп оборудования, занятых в технологических процессах рассматриваемого участка гибкого производства.
N, где N – число различных групп оборудования, занятых в технологических процессах рассматриваемого участка гибкого производства.
 |
а) б)
Рисунок 1.3.1 – а) процесс типа «механообработки»;
б) процесс типа «механосборки».
Число различных групп оборудования N совпадает с максимальным числом вершин графов технологических маршрутов (в графах технологических маршрутов число вершин может быть меньше N, это связано с тем, что при производстве некоторых модификаций продукции данного участка, определенные группы оборудования могут быть не задействованы).
Будем считать, что все группы оборудования различного типа пронумерованы.
Элементы матриц C l определены как элементы матриц смежности соответствующих графов технологических маршрутов.
Пусть далее заданы матрицы 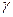
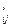 ;
; 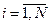 ;
; 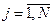 - количества единиц продукции i -ой группы оборудования, необходимые для производства продукции j -ой группы оборудования при выпуске изделий l -ой модификации.
- количества единиц продукции i -ой группы оборудования, необходимые для производства продукции j -ой группы оборудования при выпуске изделий l -ой модификации.
Для процесса типа «механообработки» справедливо равенство
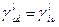
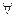
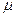 , i,
, i, 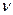 :
: 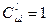 ,
, 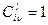 . (1.3.1)
. (1.3.1)
Для процесса типа «механосборки» равенство (1.3.1) может не выполняться.
Пусть Т 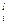 - время обработки детали продукции l -ой модификации на станке i -ой группы.
- время обработки детали продукции l -ой модификации на станке i -ой группы.
Пусть P – обобщенная стоимость выбранного технологического оборудования. Положим, что она включает в себя обычную стоимость оборудования, стоимость его установки и наладки на рассматриваемом участке.
Пусть S – площадь, необходимая для размещения на данном участке выбранного состава оборудования.
Для выпуска продукции L модификаций, необходимо выбрать такой количественный состав технологического оборудования, который обеспечит выполнение неравенств
P 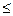 P0, S
P0, S 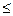 S0 (1.3.2)
S0 (1.3.2)
и в то же время позволит обеспечить выпуск намеченной продукции модификаций с заданными производительностями Г l.
В неравенствах (1.3.2) P0 и S0 – соответственно обобщенная стоимость, выделенная на технологическое оборудование для рассматриваемого участка, и полезная площадь этого участка.
Пусть К i – число станков одного типа в i -ой группе рассматриваемого технологического оборудования, 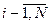 . Решить задачу выбора количественного состава оборудования, значит найти такой набор {K i },
. Решить задачу выбора количественного состава оборудования, значит найти такой набор {K i }, 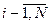 , который обеспечит выполнение неравенств (1.3.2) выпуск продукции с запланированными Г l.
, который обеспечит выполнение неравенств (1.3.2) выпуск продукции с запланированными Г l.
Далее будем рассматривать только технологический процесс типа «механосборки», так как процесс типа «механообработки» можно рассматривать как его частный случай.
Пусть вершины графов технологических маршрутов пронумерованы так, что вершина с максимальным номером соответствует последней операции l -го технологического процесса. Пусть также число технологических операций во всех технологических процессах не меньше, чем N.
Запишем уравнение баланса межгруппового обмена продукцией для N-ой вершины каждого l -го графа технологического процесса (в предположении, что обмен ведется через накапливающие устройства)
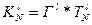 ,
, 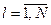 . (1.3.3)
. (1.3.3)
Здесь 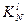 - число станков N-ой группы, необходимое для обеспечения выпуска продукции l -ой модификации с заданным Г l.
- число станков N-ой группы, необходимое для обеспечения выпуска продукции l -ой модификации с заданным Г l.
Общий вид уравнений баланса для технологического маршрута l -ой модификации можно записать в виде
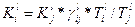 ,
, 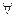
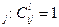 ; (1.3.4)
; (1.3.4)
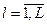 ;
; 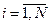 ;
; 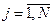 .
.
Величины 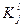 вычисляются ранее и теперь позволяют найти все
вычисляются ранее и теперь позволяют найти все 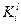 , для таких i, что
, для таких i, что 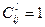 .
.
Здесь 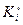 - число станков одного типа в i -ой группе рассматриваемого технологического оборудования,
- число станков одного типа в i -ой группе рассматриваемого технологического оборудования, 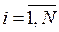 .
.
После решения уравнений баланса, найденные 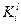 необходимо привести к целому виду
необходимо привести к целому виду
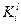 = [
= [ 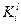 ] + 1, где [a] – целая часть а.
] + 1, где [a] – целая часть а.
Может быть ситуация когда 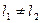 , то может получиться так, что
, то может получиться так, что 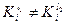 . Это означает, что при выпуске продукции различной модификации, с заданными Г l, одной и той же группе оборудования необходимо различное число единиц оборудования. Поэтому для обеспечения всех Г l,
. Это означает, что при выпуске продукции различной модификации, с заданными Г l, одной и той же группе оборудования необходимо различное число единиц оборудования. Поэтому для обеспечения всех Г l, 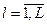 , на рассматриваемом участке, необходимо взять число станков в каждой из N групп, определенное следующим образом
, на рассматриваемом участке, необходимо взять число станков в каждой из N групп, определенное следующим образом
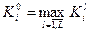 ,
, 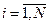 . (1.3.5)
. (1.3.5)
Пусть s i – площадь, необходимая для установки на участке одного станка i -ой группы, тогда S i = 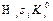 - площадь, необходимая под i -ую группу оборудования. Здесь
- площадь, необходимая под i -ую группу оборудования. Здесь 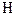 i – коэффициенты использования единицей оборудования рабочей площади участка.
i – коэффициенты использования единицей оборудования рабочей площади участка.
Необходимо, чтобы S0 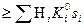 . Если S0 <
. Если S0 < 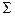 S i, то необходимо провести пересчет по площади с учетом отношения S0/
S i, то необходимо провести пересчет по площади с учетом отношения S0/ 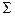 S i. Формулы пересчета:
S i. Формулы пересчета:
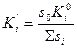 .
.
Аналогично производится пересчет по стоимости по следующей формуле 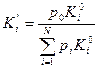 ,
,
где p i – обобщенная стоимость одного станка i -ой группы.
Пусть при пересчете по площади получено 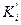 ,
, 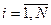 станков в группах, а при пересчете по стоимости
станков в группах, а при пересчете по стоимости 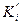 ,
, 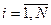 - станков, тогда для обеспечения неравенств (1.3.2) выберем количественный состав оборудования следующим образом
- станков, тогда для обеспечения неравенств (1.3.2) выберем количественный состав оборудования следующим образом
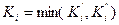 . (1.3.6)
. (1.3.6)
Новые значения Г 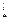 после пересчета определяются выражением
после пересчета определяются выражением
Г 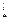 = K N / T
= K N / T 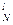 ;
; 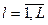
и соответствуют тем производительностям, которые возможны на рассматриваемом участке при заданных S0 и P0.
Теперь можно рассмотреть пример использования уравнений баланса.
Рассмотрим технологический участок с полезной площадью S0 = 100 и стоимостью, выделенной на оборудование P0 = 150. На участке намечен выпуск продукции трех модификаций (L = 3), и всего на участке пять различных групп оборудования (N = 5). Технологические маршруты заданы следующими матрицами
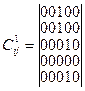 ,
, 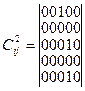 ,
, 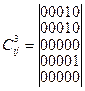
Пусть производительности будут равны Г1 = Г2 = Г3 = 10.
В соответствии с матрицам С 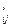 заданы матрицы производительности каждой группы оборудования
заданы матрицы производительности каждой группы оборудования 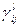
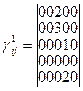 ,
, 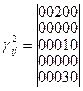 ,
, 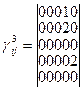
Время обработки для каждой группы оборудования заданы следующей таблицей
| l | T 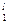 | T 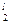 | T 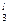 | T 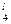 | T 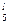 |
| 1,0 | 1,5 | 2,0 | 1,6 | 1,0 | |
| 1,2 | 1,3 | 2,0 | 1,6 | 1,0 | |
| 1,3 | 1,2 | 2,0 | 1,2 | 2,0 |
Площади и стоимости станков каждой группы заданы следующей таблицей
| N | |||||
| S | 1,0 | 1,0 | 1,5 | 2,0 | 1,2 |
| P | 1,0 | 1,5 | 2,0 | 1,0 | 0,5 |
Решая уравнения баланса, получаем следующие результаты
для l = 1 К 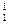 = 20, К
= 20, К 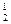 = 45, К
= 45, К 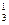 = 20, К
= 20, К 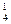 = 16, К
= 16, К 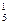 = 20;
= 20;
для l = 2 К 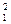 = 24, К
= 24, К 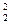 = 0, К
= 0, К 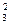 = 20, К
= 20, К 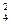 = 16, К
= 16, К 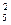 = 30;
= 30;
для l = 3 К 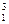 = 26, К
= 26, К 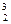 = 48, К
= 48, К 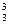 = 0, К
= 0, К 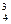 = 24, К
= 24, К 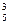 = 20.
= 20.
С учетом формулы (1.3.5) получаем состав оборудования, который обеспечит выпуск продукции всех модификаций с заданными Г l, 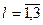
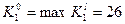 ,
, 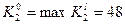 ,
, 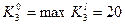 ,
,
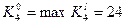 ,
, 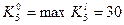 .
.
После пересчетов по площади и стоимости получим
К1 = 13, К2 = 24, К3 = 10, К4 = 12, К5 = 15.
Анализ приведенного выше примера показывает, что при выборе количественного состава оборудования методом уравнений баланса могут возникать ситуации, когда при выпуске продукции некоторых модификаций в определенных группах окажутся незадействованные станки.
Введем далее возможную схему коррекции постановки задачи выбора оборудования, допускающую ограничение простоев оборудования.
Рассмотрим выражение
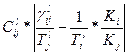 , (1.3.7)
, (1.3.7)
которое показывает величину разбаланса между i -ой и j -ой группами оборудования в пересчете на один станок j -ой группы.
Пусть на величины (1.3.7) наложены ограничения вида
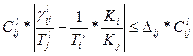 , (1.3.8)
, (1.3.8)
где Dij – задаваемые (управляемые) положительные константы, которые определяют верхнюю границу разбаланса оборудования в группах.
Ограничения (1.3.8) наложенные на количественный состав выбираемого технологического оборудования, можно представить в виде
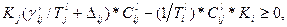
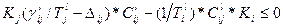 . (1.3.9)
. (1.3.9)
Введем ограничения на количественный состав выбираемого технологического оборудования для обеспечения заданных Г l.
Если задана нижняя граница производительности для выпуска продукции l -ой модификации Г 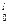 ,
, 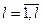 , то необходимо чтобы
, то необходимо чтобы
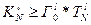 .
.
Общий вид ограничений на количественный состав
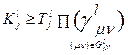 ,
,
где 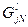 - множество вершин l -го технологического маршрута, лежащих на пути из вершины j в вершину N.
- множество вершин l -го технологического маршрута, лежащих на пути из вершины j в вершину N.
Для обеспечения Г l при любом l на одном и том же составе технологического оборудования, необходимо чтобы
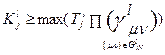 . (1.3.10)
. (1.3.10)
Далее на выбор количественного состава оборудования накладываются дополнительные ограничения с учетом времени переналадки.
Будем считать, что набор модификаций пронумерован. Пусть задана последовательность 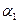 ,
, 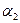 , …,
, …, 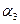 выпуска продукции участка. Каждое
выпуска продукции участка. Каждое 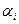 ,
, 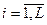 соответствует продукции одной из L модификаций.
соответствует продукции одной из L модификаций.
Пусть T 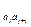 – время, необходимое для перевода участка с выпуска продукции
– время, необходимое для перевода участка с выпуска продукции 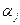 -ой модификации на продукцию
-ой модификации на продукцию 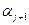 -ой модификации.
-ой модификации.
Пусть Т – время, выделенное на выполнение последовательности, 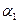 ,
, 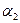 , …,
, …, 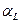 , а t l – время, выделенное из времени Т на выпуск продукции l -ой модификации.
, а t l – время, выделенное из времени Т на выпуск продукции l -ой модификации.
С учетом времени переналадки, получаем
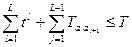 . (1.3.11)
. (1.3.11)
Пусть T 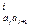 – время, необходимое на переналадку одного станка i –ой группы при переходе с выпуска продукции
– время, необходимое на переналадку одного станка i –ой группы при переходе с выпуска продукции 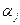 -ой модификации на выпуск продукции
-ой модификации на выпуск продукции 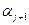 -ой модификации.
-ой модификации.
Рассмотрим вариант последовательной перенастройки технологического оборудования. В этом случае можно записать
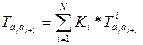 . (1.3.12)
. (1.3.12)
Тогда неравенство (1.3.11) можно переписать с учетом (1.3.12)
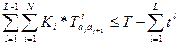 . (1.3.13)
. (1.3.13)
Поставим задачу выбора количественного состава технологического оборудования с учетом разбаланса между группами и времени переналадки оборудования:
минимизировать функцию
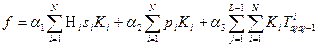 (1.3.14)
(1.3.14)
при условиях
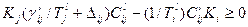 ,
,
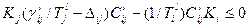 ,
,
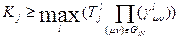 .
.
Задача (1.3.14) является задачей линейного программирования и может быть решена известными методами, например, симплекс-методом /5/.
Далее рассмотрим вкратце сам симплекс-метод.
 2015-06-10
2015-06-10 1301
1301







