Условие принадлежности четырех точек одной плоскости

Смешанное произведение векторов, заданных своими декартовыми координатами

Три вектора 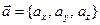, , 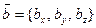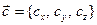заданы своими декартовыми координатами. Разложим их по ортам : , , .

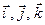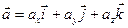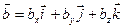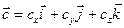Известно, что векторное произведение векторов 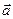и 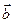находится по формуле:

.

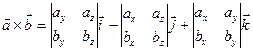Найдем скалярное произведение вектора векторного произведения 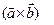и вектора 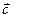, как векторов, декартовые координаты которых известны:

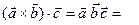
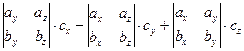– это есть разложение по третьей строке определителя 3-го порядка:

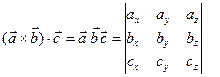– формула для вычисления смешанного произведения векторов, заданных своими декартовыми координатами

Условие принадлежности четырех точек одной плоскости

Задача. Даны 4 точки , , , .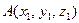

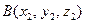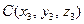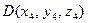Доказать, что данные точки лежат в одной плоскости .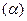

Доказательство.

Составим три вектора: 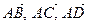такие, что , , .

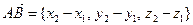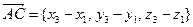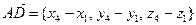Из 2-го свойства смешанного произведения следует, что три вектора компланарны только тогда, когда их смешанное произведение равно нулю:

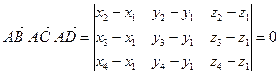– условие принадлежности четырех точек одной плоскости.