ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ВАРИАНТ 2
Задача 1. Докажите, что при любом натуральном 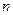 имеет место равенство
имеет место равенство 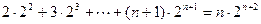 .
.
Задача 2. Докажите, что при любом натуральном 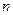
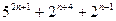 делится на 23.
делится на 23.
Задача 3. Сколькими способами можно составить подарочный комплект из трех книг по архитектуре и трех книг по искусству, если можно выбрать любую из 6 книг по архитектуре и любую из 5 книг по искусству?
Задача 4. Найдите коэффициент при 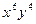 в разложении
в разложении 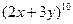 .
.
Задача 5. Даны числовые множества 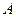 и
и 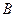 . Найдите
. Найдите 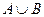 ,
, 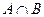 ,
, 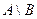 ,
, 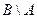 ,
, 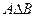 ,
, 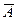 и
и 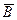 . Изобразите
. Изобразите 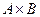 .
.
а) 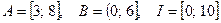 ,
,
б) 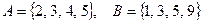 , где
, где 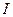 — множество цифр
— множество цифр 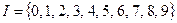 .
.
Задача 6. Каждый из 45 туристов, прибывших в Мон-Сен-Мишель, свое свободное время посвятил посещению старого бенедиктинского аббатства, покупке сувениров и поеданию устриц в местном ресторанчике. Аббатство посетило 28 человек, сувениры приобрели 18, а устрицами успели полакомиться 14 человек; из посетивших аббатство лакомились устрицами 6, попробовали устриц и купили сувениры 7,посетили аббатство и купили сувениры — 4. Сколько человек успели осмотреть исторические достопримечательности, попробовать местные деликатесы и купить сувениры на память, а сколько успели только посетить аббатство?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение 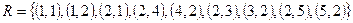 на множестве
на множестве 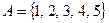 . Запишите матрицу отношения
. Запишите матрицу отношения 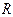 и постройте граф.
и постройте граф.
Задача 8. На множестве действительных чисел задана операция 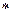 по формуле
по формуле 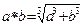 . Проверьте, является ли она коммутативной, ассоциативной.
. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежутками 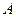 и
и 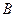 аналитически, если
аналитически, если 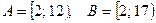 .
.
 2015-06-26
2015-06-26 713
713








