Отношения. Фундаментальным понятием дискретной математики является понятие отношения, которое используют для обозначения связи между объектами или понятиями

Фундаментальным понятием дискретной математики является понятие отношения, которое используют для обозначения связи между объектами или понятиями.

Квадратом множества М называется декартово произведение двух равных между собой множеств: М 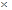М = М². Бинарным отношением Т в множестве М называется подмножество его квадрата: .

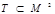элементы т_i, и т_j, находятся в отношении T, если .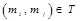

Граф

Совокупность множества М с заданным в нем бинарным отношением 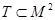называется графом G:

,

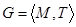где М - носитель графа (множество вершин); Т - сигнатура графа (множество дуг).

Рассмотрим задание бинарного отношения с помощью матрицы смежности и фактор-множества.

При матричном задании используют двумерную таблицу — матрицу смежности, каждой строке (столбцу) которой взаимно однозначно сопоставляют элемент множества М. Тогда каждая клетка (i, j) взаимно однозначно соответствует элементам множества М². Клетку (i, j), которая соответствует элементу, принадлежащему 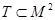, как-то отличают, например зачерняют или помещают в нее единицу; остальные клетки оставляют незачерненными или записывают в них нули.