Группоид

Алгебра вида <М, f₂> называется группоидом.

Если f₂ — операция типа умножения (Ч), то группоид называют мультипликативным, если f₂ - операция типа сложения (+), то аддитивным.

Пусть А = <М, f₂) — группоид; обозначим операцию f₂ как 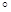. Тогда элемент 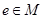называется правым нейтральным элементом группоида А, если для всякого 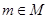выполняется равенство т 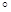е = т; элемент 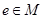группоида А = <М, 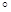> называется левым нейтральным элементом, если для всех 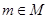выполняется равенство е 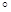т = т. В этих определениях использовались выражения «все элементы», «всякий элемент». В дальнейшем для краткости вместо слов «все» или «всякий» будем использовать символ 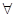(перевернутая буква А — первая буква английского слова All — все). Если элемент е, 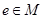, группоида А = <М, 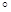> является одновременно левым и правым нейтральным элементом, то его называют двусторонним нейтральным элементом или просто нейтральным элементом.

Никакой группоид не может иметь более одного нейтрального элемента. Действительно, если

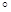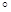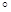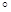т е = е т = т и т е'=е' т=т

справедливо для всех 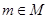, то

е' = е' 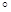е = е.

Если группоид <М, 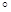> мультипликативный, то нейтральный элемент называется единицей и обозначается 1; если аддитивный, то нейтральный элемент называется нулем и обозначается 0.

Группоид А = <М, 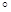> называется идемпотентным, если его сигнатура удовлетворяет закону идемпотентности

.

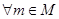
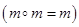Группоид <М, 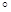>, сигнатура которого удовлетворяет закону коммутативности

.

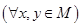
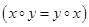называется коммутативным или абелевым.

Группоид <М, 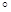>, в котором выполняется закон ассоциативности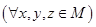 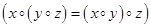называется ассоциативным или полугруппой.

Группа

Полугруппа <М, 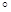> в которой выполнимы обратные операции: для любых 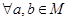каждое из уравнений 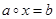, 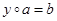обладает единственным решением, называется группой.

Пример.

Рассмотрим понятие группы на примере группы подстановок, содержащей шесть элементов. Группу подстановок исследовал выдающийся французский математик Галуа в связи с решением уравнений в радикалах.

Подстановкой n -й степени называется взаимно однозначное отображение множества из п элементов на себя.

Рассмотрим три элемента: х₁, х₂, х₃. Существует шесть перестановок из трех элементов (3! = 6): х₁х₂х₃, х₂х₃х₁, х₁х₂х₃, х₃х₁х₂, х₂х₁х₃, х₃х₂х₁. Запишем две перестановки из трех элементов друг под другом:

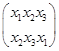
Эта запись означает, что х₁ переходит в х₂, х₂ - в х₃, х₃ – в х₁.

Число возможных подстановок равно числу перестановок. Введем следующие обозначения для шести возможных подстановок:

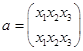
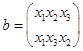
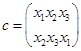
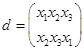
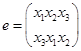
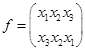
Введем операцию умножения 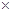над подстановками.

Произведением подстановок называется подстановка, получаемая в результате последовательного выполнения сначала первой, а затем второй из перемноженных подстановок. Например,

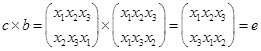
Выражение α 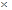β, α,β = а, b, с, d, е, f определяет табл. 1.1.

Таблица 1.1

α	β
а	b	с	d	е	f
a	а	b	с	d	е	f
b	b	а	d	с	f	е
c	с	е	а	f	b	d
d	d	f	b	е	а	с
е	е	с	f	а	d	b
f	f	d	е	b	с	а

В рассматриваемой алгебре <М, Ч> выполняется закон ассоциативности, но не выполняется закон коммутативности.