Выполнение арифметических операций с двоичными числами

В машинной арифметике знак «+» числа принято кодировать цифрой 0, а знак «-» принято кодировать цифрой 1. Положительные числа хранятся в ЭВМ в прямом коде (вышеописанном), перед ними ставится знак 0. Отрицательные числа хранятся в так называемом дополнительном коде.

Рассмотрим правило кодирования отрицательных чисел в дополнительном коде. Число сначала записывается в обратном коде, а затем к самому младшему разряду прибавляется 1. Обратный код числа получается из прямого кода числа при порязрядной замене 1 на 0 и 0 на 1.

Пример (здесь знак числа отделен символом ‘|’):

+83₁₀=0|1010011₂.- в прямом коде

-83₁₀=1|0101100₂- в обратном коде

-83₁₀=1|0101100₂+1₂=1|0101101₂- в дополнительном коде.

Использоваие дополнительного кода при представлении отрицательного числа позволяет свести операцию вычитания чисел к операции арифметического сложения их кодов, облегчает выработку признаков переполнения разрядной сетки и, в конечном счете, упрощает устройства ЭВМ.

Сложение

Для этого нужно знать простейшую таблицу

а). 0 + 0 = 0

б). 0 + 1 = 1 + 0 = 1

в). 1 + 1 = 10

Последнее означает, что при сложении двух двоичных чисел, равных 1 в каком-либо разряде двоичного числа, возникает перенос в старший разряд.

Пример:

⁺ 1001111

10111100

Вычитание

Таблица вычитания двоичных чисел имеет вид:

а). 0 - 0 = 0

б). 1 - 0 = 1

в). 1 - 1 = 0

г). 10 - 1 = 1 и в общем случае .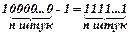

Если при поразрядном вычитании приходится вычитать из нуля в уменьшаемом единицу в вычитаемом, то делается заем в соседнем старшем разряде, т. е. единица старшего разряда представляется как 2 единицы данного разряда.

Пример:

^- 10110110

Умножение

Умножение двух двоичных чисел выполняется так же, как и умножение двух десятичных (столбиком), т. е. множимое последовательно умножается на каждую цифру множителя, начиная с младшей (либо со старшей), и, для учета веса соответствующей цифры множителя, сдвигается либо влево, если умножение производится, начиная с младшего разряда множителя, либо вправо, если умножение производится, начиная со старшего разряда множителя, на такое число разрядов, на какое соответствующий разряд множителя сдвинут относительно младшего или старшего разряда соответственно. Получающиеся в результате умножения и сдвига частичные произведения после суммирования дают полное произведение. Отличительная особенность, значительно облегчающая умножение двоичных чисел по сравнению с умножением десятичных чисел, заключается в том, что частичное произведение может быть только 0 (если соответствующая цифра множителя равна 0), либо сдвинутым на соответствующее число разрядов множимым (если соотвтетствующая цифра множителя равна 1).

Пример (умножение двух двоичных чисел, начиная с младших разрядов множителя):

^* 1011

+ 110101

1001000111

Тот же результат может быть получен при умножении, начиная со старших разрядов множителя:

^* 1011

+ 110101

1001000111

Если множимое или множитель, или оба вместе содержат не только целую, но и дробную часть, то запятые в множимом и множителе зачеркиваются, полученные два целых двоичных числа умножаются друг на друга и от полученного произведения справа отделяются запятой (m + n) разрядов, где m - количество дробных разрядов множимого, а n - количество дробных разрядов множителя.

Деление

Деление двух двоичных целых чисел выполняется аналогично делению десятичных чисел. Рассмотрим деление целого делимого на целый делитель, так как случай, когда делимое и (или) делитель содержат дробные члены, легко может быть сведен к делению целых чисел путем одновременного умножения делимого и делителя на одно и то же число, равное целой степени двойки. Это легко сделать путем добавления к дробной части делимого или делителя такого количества нулей, чтобы дробная часть обоих членов имела одинаковое количество разрядов, и зачеркивания запятой в обоих числах.

Примеры:

11010111 10110 1011001.00 11011010