Система изображения любых чисел с помощью ограниченного числа знаков называется СС.
Известно, что от выбора СС в значительной степени зависит удобство выполнения арифметических операций с помощью карандаша и бумаги. В случае выполнения вычислений на ЦВМ выбор СС в большой степени определяет ее конструкцию, схемы основных элементов и узлов, скорость выполнения операций. Поэтому вопросу о правильном выборе СС для реализации ее на ЦВМ необходимо уделять особое внимание.
В позиционных СС целое число, изображенное в виде
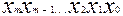 ,
,
равно
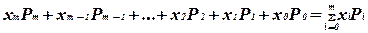 ,
,
где 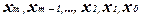 - символы, обозначающие целые числа;
- символы, обозначающие целые числа; 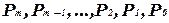 - веса, то есть количественные значения каждой единицы, определяемое местом (позицией), занимаемым соответствующим символом в изображении числа.
- веса, то есть количественные значения каждой единицы, определяемое местом (позицией), занимаемым соответствующим символом в изображении числа.
Номер позиции, определяющий вес единицы, расположенной на этой позиции, называется разрядом.
Среди позиционных СС особое значение имеют СС, в которых веса отдельных разрядов представляют собой ряд членов геометрической прогрессии со знаменателем p. В этом случае число
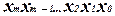 ,
, 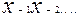
(номер разряда отсчитывается от запятой) имеет значение
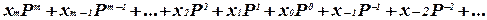
 .
.
Число различных символов, необходимых для записи произвольного числа, равно знаменателю геометрической прогрессии p. В большинстве случаев бывает удобно использовать целые числа натурального ряда от 0 до p -1.
Знаменатель геометрической прогрессии p, равный отношению веса любого разряда к весу соседнего разряда справа, носит название основания СС.
Позиционный способ записи чисел не является единственно возможным. Примером непозиционной СС является система римской нумерации. Основным преимуществом позиционной СС следует считать удобство выполнения таких арифметических операций как сложение, вычитание, умножение, деление, извлечение корня и других.
Выбор числа десять в качестве основания СС исторически связан с числом пальцев на руках человека. Однако десятичная СС не является наиболее удобной с точки зрения ее реализации в ЦВМ. Любой из символов, применяемых для записи чисел, должен в ЦВМ изображаться в виде одного из нескольких возможных состояний некоторого физического элемента. Естественно, что эти состояния должны быть устойчивы и четко различимы.
Выполнение элемента с десятью четко различимыми состояниями представляет собой достаточно сложную техническую задачу, в то время как элементов с 2-я четко различимыми состояниями имеется достаточно много. Указанное обстоятельство явилось одной из главных причин широкого распространения двоичной СС в цифровой технике.
В то же время для человеческого восприятия гораздо более приемлемой оказывается запись числа не в двоичной, а в СС с основаниями 10, 16 или 8. Поэтому общепринятой является следующая схема использования СС:
* при вводе чисел в ЦВМ применяют чаще всего десятичную, затем шестнадцатеричную, восьмеричную и реже всего - двоичную СС;
* введенные числа преобразуются внутри ЦВМ в двоичные числа и в таком виде обрабатываются;
* выводимые значения, как правило, опять преобразуют из двоичной формы представления в десятичную, шестнадцатеричную или восьмеричную. Поэтому знание технологии преобразования формы представления чисел из одной СС в другую имеет при изучении данного курса фундаментальное значение.
В нижеследующей таблице 1 представлены некоторые десятичные числа в двоичной СС.
Преимущества двоичной СС состоят в:
* простоте выполнения арифметических операций;
Таблица 1





 Десятичное Двоичное Десятичное Двоичное
Десятичное Двоичное Десятичное Двоичное
изображение изображение изображение изображение
числа числа числа числа
0 0 1/2 (0.5) 0,1
 1 1 1/4 (0.25) 0,01
1 1 1/4 (0.25) 0,01
 2 10 3/4 (0.75) 0,11
2 10 3/4 (0.75) 0,11
3 11 1/8 (0.125) 0,001
4 100 1/16 (0.0625) 0,0001
5 101 3/16 (0.1875) 0,0011
7 111 11/16 (0.6875) 0,1011
8 1000 3 5/16 (3.3125) 11,0101
16 10000 1 3/8 (1.375) 1,011
25 11001
* экономичности.
Под экономичностью СС понимается число цифро-разрядов, необходимых для изображения натурального ряда ряда целых чисел в пределах от 0 до N.
 2015-06-26
2015-06-26 471
471







