Пусть 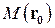 – некоторая точка плоскости
– некоторая точка плоскости 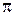 , а
, а 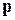 и
и 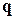 – направляющие векторы плоскости, т. е. неколлинеарные векторы, параллельные этой плоскости. Тогда вектор
– направляющие векторы плоскости, т. е. неколлинеарные векторы, параллельные этой плоскости. Тогда вектор 
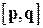 может быть принят за нормальный вектор. С учетом (4.1) это приводит нас к векторному уравнению вида
может быть принят за нормальный вектор. С учетом (4.1) это приводит нас к векторному уравнению вида
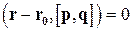
или
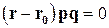 . (4.6)
. (4.6)
Отметим, что условие (4.6) есть условие компланарности векторов 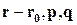 .
.
Пусть в произвольной прямоугольной декартовой системе координат
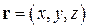 ,
, 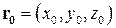 ,
, 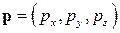 ,
, 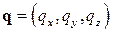 .
.
Тогда уравнение (4.6) можно записать так:
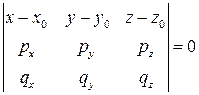 . (4.7)
. (4.7)
Условие (4.6) вследствие неколлинеарности векторов 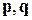 можно записать в виде
можно записать в виде
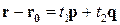
или
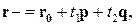
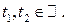
Это уравнение называется векторно-параметрическим уравнением плоскости. Вектор 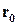 называется вектором сдвига плоскости.
называется вектором сдвига плоскости.
В координатах уравнение (4.8) примет вид
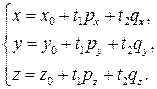
Уравнение плоскости, проходящей через три точки 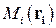 ,
, 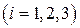 ,
,
 2015-06-28
2015-06-28 335
335








