Рассмотрим частные случаи уравнения плоскости
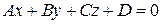 . (4.9)
. (4.9)
1. 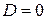 . Плоскость проходит через начало координат (его координаты
. Плоскость проходит через начало координат (его координаты 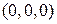 удовлетворяют уравнению плоскости).
удовлетворяют уравнению плоскости).
2. Все коэффициенты 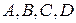 отличны от нуля. В этом случае можно поделить обе части уравнения (4.9) на
отличны от нуля. В этом случае можно поделить обе части уравнения (4.9) на 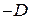 . Полагая
. Полагая
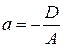 ,
, 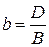 ,
, 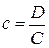 ,
,
получаем уравнение плоскости в виде:
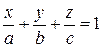 . (4.10)
. (4.10)
Числа 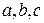 с точностью до знака равны отрезкам, отсекаемым плоскостью на осях координат. Действительно, при
с точностью до знака равны отрезкам, отсекаемым плоскостью на осях координат. Действительно, при 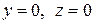 из уравнения (9.10) получаем
из уравнения (9.10) получаем 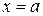 , т. е. плоскость пересекает ось
, т. е. плоскость пересекает ось 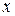 в точке
в точке 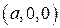 и т.д. Уравнение (9.10) называется уравнением плоскости в отрезках на осях.
и т.д. Уравнение (9.10) называется уравнением плоскости в отрезках на осях.
3. 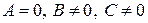 . Вектор
. Вектор 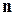 (перпендикулярный плоскости) перпендикулярен оси
(перпендикулярный плоскости) перпендикулярен оси 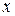 . Значит, плоскость параллельна оси
. Значит, плоскость параллельна оси 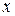 , в частности проходит через нее, если
, в частности проходит через нее, если 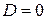 .
.
4. 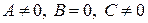 . Вектор
. Вектор 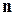 (перпендикулярный плоскости) перпендикулярен оси
(перпендикулярный плоскости) перпендикулярен оси 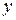 . Значит, плоскость параллельна оси
. Значит, плоскость параллельна оси 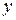 , в частности проходит через нее, если
, в частности проходит через нее, если 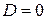 .
.
5. 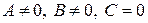 . Вектор
. Вектор 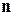 (перпендикулярный плоскости) перпендикулярен оси
(перпендикулярный плоскости) перпендикулярен оси 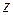 . Значит, плоскость параллельна оси
. Значит, плоскость параллельна оси 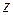 , в частности проходит через нее, если
, в частности проходит через нее, если 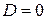 .
.
6. 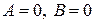 . Вектор
. Вектор 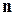 параллелен оси
параллелен оси 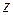 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости 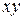 , в частности совпадает с плоскостью
, в частности совпадает с плоскостью 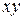 , если
, если 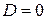 .
.
7. 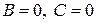 . Вектор
. Вектор 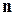 параллелен оси
параллелен оси 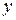 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости 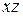 , в частности совпадает с плоскостью
, в частности совпадает с плоскостью 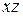 , если и
, если и 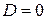 .
.
8. 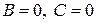 . Вектор
. Вектор 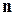 параллелен оси
параллелен оси 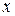 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости 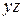 , в частности, совпадает с плоскостью
, в частности, совпадает с плоскостью 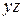 , если и
, если и 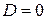 .
.
 2015-06-28
2015-06-28 422
422








