2015-06-28
322
Существует, причем единственная, плоскость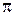 
, перпендикулярная заданному вектору 
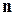и содержащая данную точку 
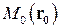. Всякий вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости. Для произвольной точки 
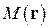пространства (рис. 8) имеем логическую цепочку
.
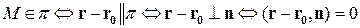Уравнение
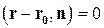(4.1)
называется векторным уравнением плоскости.
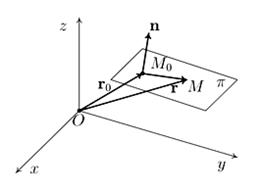
Рис. 8. Плоскость в пространстве
Уравнению (4.1) можно придать форму
,
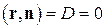где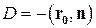 
. Такое уравнение не содержит радиус-вектора начальной точки.
Рассмотрим уравнение (4.1) при наличии прямоугольной декартовой системы координат. Пусть
, 
.
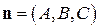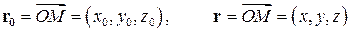Тогда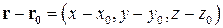 
и (4.1) примет вид
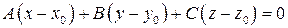. (4.2)
Итак, в прямоугольной системе координат плоскость, проходящая через точку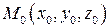 
и перпендикулярная вектору 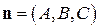, задается уравнением (4.2).
