Лекция 4. Плоскость в пространстве
Декартова прямоугольная система координат. Уравнение плоскости, проходящей через данную точку и перпендикулярной данному вектору. Линейное уравнение. Различные виды уравнения плоскости. Расположение плоскости относительно координатных осей. Расстояние от точки до плоскости. Нормированное уравнение плоскости.
Декартова прямоугольная система координат в пространстве
Зафиксируем в пространстве точку 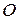 и рассмотрим произвольную точку
и рассмотрим произвольную точку 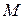 . Радиус-вектором
. Радиус-вектором 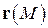 точки
точки 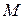 называется вектор
называется вектор 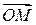 . Точку
. Точку 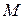 , задаваемую радиус-вектором
, задаваемую радиус-вектором 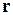 , будем обозначать
, будем обозначать 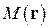 . Пусть имеется также некоторый ортонормированный базис
. Пусть имеется также некоторый ортонормированный базис 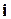 ,
, 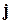 ,
, 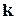 . Будем считать, что вектора
. Будем считать, что вектора 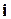 ,
, 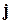 ,
, 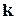 выходят из точки
выходят из точки 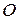 . Проведем через эти вектора оси
. Проведем через эти вектора оси 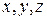 . Совокупность
. Совокупность 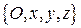 точки
точки 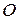 начала координат и координатных осей
начала координат и координатных осей 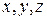 называется прямоугольной декартовой системой координат.
называется прямоугольной декартовой системой координат.
Произвольной точке 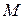 ставится в соответствие единственная упорядоченная тройка чисел
ставится в соответствие единственная упорядоченная тройка чисел 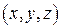 – координаты ее радиус-вектора
– координаты ее радиус-вектора 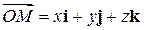 . В краткой записи
. В краткой записи
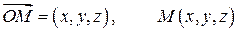 .
.
 2015-06-28
2015-06-28 336
336







