2015-06-28
272
Уравнение (4.2) легко преобразовать к виду
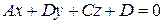. (4.3)
Покажем, что любое такое уравнение (при очевидном условии)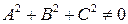 
задает в прямоугольной декартовой системе 
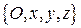координат плоскость.
Пусть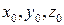 
– какое-нибудь решение уравнения (4.3), т. е.
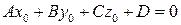. (4.4)
Вычитая (4.4) из (4.3), получим равносильное (4.3) уравнение
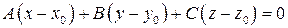. (4.5)
Пусть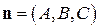 
, 
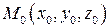и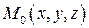 
. Тогда (4.5) можно записать в эквивалентной форме:
.
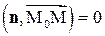Таким образом, все точки плоскости, проходящей через точку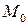 
и перпендикулярной вектору 
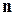(и только они), удовлетворяют уравнению (4.3). Следовательно, (4.3) является уравнением этой плоскости.
Отметим еще раз, что коэффициенты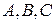 
в уравнении плоскости (4.3) суть координаты вектора, перпендикулярного плоскости.
Уравнение плоскости, проходящей через данную точку
