3.1. Сила 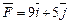 разложена по двум перпендикулярным направлениям, одно из которых задано вектором
разложена по двум перпендикулярным направлениям, одно из которых задано вектором 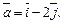 Найдите направляющую силы в направлении этого вектора.
Найдите направляющую силы в направлении этого вектора.
3.2. Подберите ненулевые числа α, β, γ так, чтобы
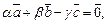 где
где 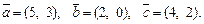
3.3. Даны три вершины А (3, –4), В (–5, 3) и С (1, 2) параллелограмма ABCD. Найдите его четвертую вершину D.
3.4. Даны вершины треугольника А (3, –1), В (4, 2) и С (–4, 0). Найдите длину медианы, проведенной из вершины А.
3.5. Даны вершины А (1, –1), В (2, 1) и С (–5, 2) треугольника АВС. Вычислите длину биссектрисы его внутреннего угла при вершине А.
3.6. Треугольник АВС задан координатами своих вершин: А (3, –2), В (3, 1) и С (4, 0). Вычислите расстояние от начала координат до точки пересечения медиан этого треугольника.
3.7. В вершинах треугольника А (1, –1), В (0, 4) и С (2, –1) сосредоточены массы соответственно 1, 2, 3. Найдите координаты центра масс этой системы.
З а м е ч а н и е. Для пары масс m 1 и m 2, сосредоточенных в точках А и В, центр находится в точке, делящей отрезок АВ в отношении 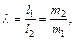 где l1 и l2 – расстояния от точек с соответствующими массами до их центра.
где l1 и l2 – расстояния от точек с соответствующими массами до их центра.
3.8. Даны векторы 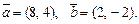 Найдите вектор
Найдите вектор 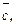 лежащий с векторами
лежащий с векторами 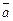 и
и 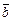 в одной плоскости, перпендикулярный вектору
в одной плоскости, перпендикулярный вектору 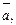 равный ему по длине и образующий с вектором
равный ему по длине и образующий с вектором 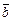 тупой угол.
тупой угол.
3.9. Представьте ненулевой вектор 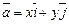 в виде линейной комбинации векторов
в виде линейной комбинации векторов 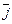 и
и 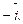
 2015-06-28
2015-06-28 864
864








