Алферьева М. АВБ. Прямые и плоскости

Акулов Д. АВБ. Прямые и плоскости

ВАРИАНТ 1

Задача 1. Дано: М₁(0; 4); М₂(10; 3); φ= 30⁰; 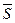= (3; 2); 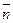= (4; -3);

L₁: 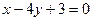; L₂: .

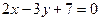1. Написать общие уравнения прямых, проходящих через

а) точку 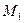под углом 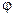к оси ;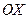

б) точк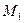и и ;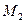

в) точку 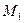параллельно вектору ;

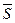г) точку 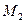перпендикулярно вектору ;

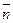д) точку 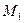параллельно прямой ;

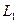е) точку 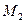перпендикулярно прямой .

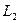2.Найти расстояние от точки 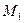до прямой 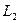с точностью до 0,01.

3. Найти а) точку пересечения прямых 5) и 6),

б) найти угол между ними с точностью до 0,1⁰.

Задача 2. Даны вершины тетраэдра :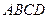

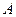(3; 4; -1), 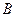(5; 2; 2), 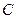(3; 1; 0), 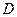(2; 0; -3).

1. Написать

а) уравнение плоскости ;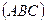

б) уравнение плоскости, проходящей через 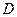параллельно ;

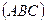в) канонические и параметрические уравнения ребра ;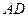

г) канонические и параметрические уравнения прямой, содержащей высоту 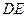тетраэдра.

2. Найти

а) угол между 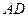и 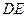с точностью до 0,1⁰;

б) площадь треугольника ;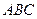

в) объем тетраэдра;

г) высоту 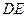с точностью до 0,01;

д) координаты точки 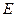с точностью до 0,01.

Задача 3. Написать уравнение плоскости, проходящей через точк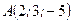и и 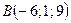перпендикулярно плоскости .

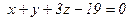Задача 4. Написать уравнение диагонали 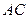параллелограмма 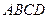, Сли даны уравнения сторон: 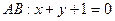и 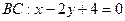и точка пересечения диагоналей .

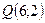Алферьева М. АВБ. Прямые и плоскости

ВАРИАНТ 2

Задача 1. Дано: М₁(0; -6); М₂(6; 4); φ= 45⁰; 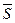= (5; 3); 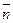= (1; 2);

L₁: 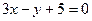; L₂: .

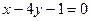1. Написать общие уравнения прямых, проходящих через

а) точку 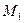под углом 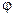к оси ;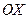

б) точк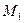и и ;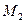

в) точку 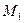параллельно вектору ;

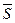г) точку 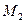перпендикулярно вектору ;

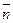д) точку 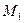параллельно прямой ;

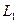е) точку 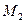перпендикулярно прямой .

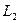2.Найти расстояние от точки 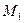до прямой 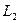с точностью до 0,01.

3. Найти а) точку пересечения прямых 5) и 6),

б) найти угол между ними с точностью до 0,1⁰.

Задача 2. Даны вершины тетраэдра :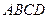

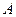(1; 3; 3), 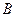(-5; 0; 1), 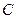(4; 2; -2), 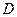(3; -1; 4).

1. Написать

а) уравнение плоскости ;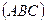

б) уравнение плоскости, проходящей через 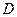параллельно ;

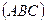в) канонические и параметрические уравнения ребра ;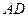

г) канонические и параметрические уравнения прямой, содержащей высоту 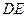тетраэдра.

2. Найти

а) угол между 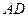и 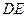с точностью до 0,1⁰;

б) площадь треугольника ;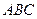

в) объем тетраэдра;

г) высоту 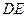с точностью до 0,01;

д) координаты точки 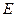с точностью до 0,01.

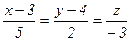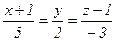Задача 3. Написать уравнение плоскости, проходящей параллельно плоскости прямых и через точку .

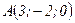Задача 4. Написать уравнение сторон треугольника, зная одну его вершину 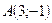, а также уравнение биссектрисы 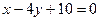и медианы 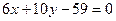, проведенных из различных вершин.