2015-06-28
226
15. Каноническое уравнение окружности с центром в точке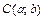 
и радиуса 
: 
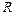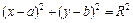(рис. 1).
16. Для параболы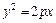 
точка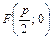 
– фокус и прямая 
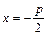– директриса. Для параболы 
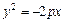фокусом является точка 
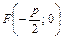, а директрисой – прямая 
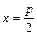. Парабола 
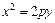имеет фокус в точке 
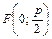, а директрисой служит прямая 
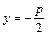. Для параболы 
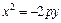точка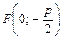 
– фокус и прямая 
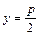– директриса (рис. 2).
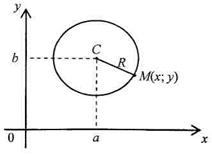Рис. 1
| 
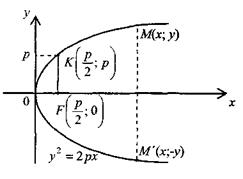Рис. 2
|
17. Каноническое уравнение эллипса: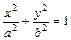 
(рис. 3). Точки 
, 
, 
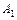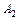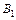и 
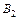– вершины эллипса; отрезок 
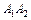и его длина 
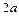– большая ось, отрезок 
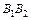и его длина 
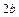– малая ось; числа 
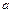и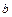 
– большая и малая полуоси; точк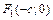и 
и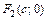 
– левый и правый фокусы; число 
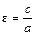– эксцентриситет; 
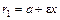и 
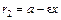– левый и правый фокальные радиусы; параметры 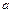, 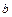и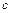 
связаны равенством 
.
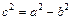18. Каноническое уравнение гиперболы: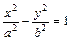 
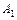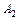(рис. 4). Точки и – вершины гиперболы; отрезок 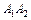и его длина 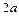– действительная ось, отрезок 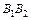и его длина 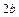– мнимая ось; числа 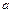и 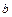– действительная и мнимая полуоси; точк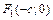и и 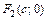– левый и правый фокусы; число 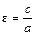– эксцентриситет гиперболы; левый и правый фокальные радиусы для точек левой ветви гиперболы равны 
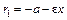и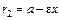 
, а для точек правой ветви гиперболы – 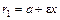и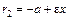 
; прямые 
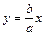и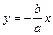 
– асимптоты гиперболы; параметры 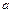, 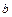и 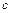связаны равенством 
.
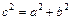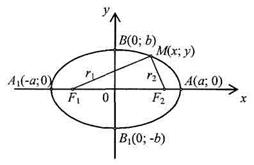Рис. 3
| 
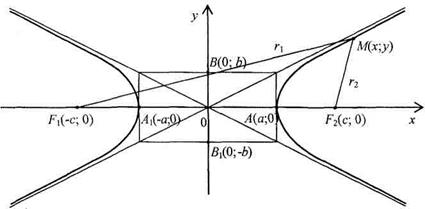Рис. 4
|
