Полный четырёхвершинник

Определение 1: полным четырёхвершинником (или полным четырёхугольником) называется фигура, образованная четырьмя точками, никакие три из которых не лежат на одной прямой, и шестью прямыми, попарно соединяющими эти точки.

Указанные четыре точки называются вершинами, а шесть прямых называются сторонами полного четырёхвершинника.

Две стороны, не имеющие общей вершины, называются противоположными.

Три точки пересечения противоположных сторон называются диагональными точками, а три прямые, попарно соединяющие диагональные точки, называются диагоналями.

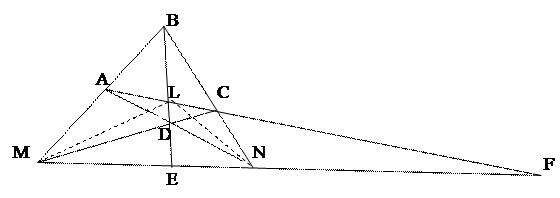ABCD – полный четырёхвершинник.

A, B, C, D – вершины; AB, BC, CD, AD, AC, BD – стороны.

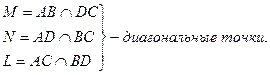
MN, ML, NL – диагонали.

MNL – дигональный трёхвершинник.

Доказательство:

Выберем на проективной плоскости 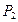проективный репер R=(A; B; C; D) и найдем координаты диагональных точек M, N, L в этом репере как точек пересечения соответственных противоположных сторон: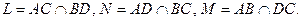

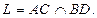
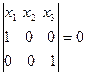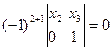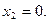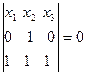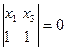Прямая АС в репере R имеет уравнение: или или Прямая BD в репере R имеет уравнение: или или 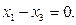Точка L определяется из системы: 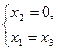и имеет координаты: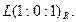

Аналогично находим координаты двух других диагональных точек: 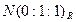и .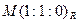

Так как 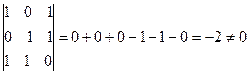, то по теореме 2 §8 точки M, N, L не лежат на одной прямой.

Теорема: на каждой диагонали полного четырёхвершинника расположена гармоничная четвёрка точек, образованная:

1) Двумя диагональными точками;

2) Двумя точками пересечения этой диагонали со сторонами, проходящими через третью диагональною точку.

Например,

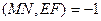(1)

Доказательство:

Спроектируем точки M, N, E, F из центра В на сторону АС.

По теореме 4 из §13 двойное отношение при этом не изменится:

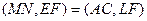(2)

Теперь точки 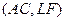спроектируем из центра D на диагональ MN. Аналогично получим:

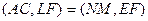(3)

Сравнивая (2) и (3), имеем:

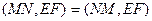(4)

По следствию 1 из теоремы 1 предыдущего параграфа:

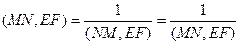(5)

Из равенства (5) получаем 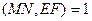или 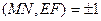. Если предположить, что 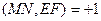, то по заключению 1 к определению 1 из §13 две из этих точек совпадают, поэтому совпадают две стороны четырёхвершинника ABCD, а точки A, B, C, D лежат на одной прямой. Это противоречит определению полного четырёхвершинника.

Поэтому .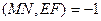

Следствие: на каждой стороне полного четырёхвершинника расположена гармоничная четвёрка точек, состоящая из двух его вершин, диагональной точки и точки пересечения этих стороны с диагональю, проходящей через две остальные диагональные точки.

Доказательство: вытекает из равенств (1) и (2).

Пример 1: построить точку F, гармонически сопряжённую с точкой E относительно точек M и N (то есть построить четвёртую гармоническую точку к трём данным).

Дано: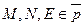

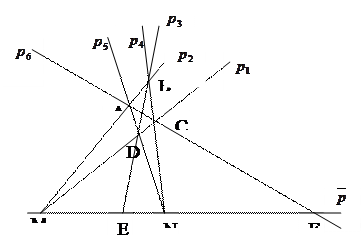Построение:

1) 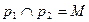- произвольно;

2) 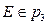- произвольно;

3) ;

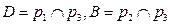4) ;

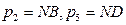5) ;

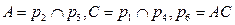6) 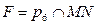- искомая точка.

Доказательство:

Согласно теореме имеем: .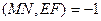

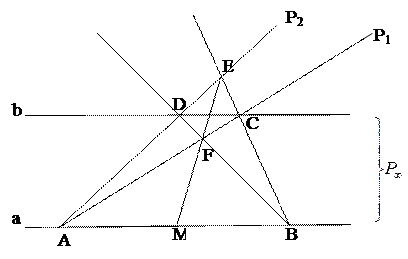
Пример 2: наЕ₂ даны две параллельные прямые 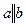и отрезок АВ на прямой а. С помощью одной линейки разделить его пополам (или построить середину М).

Дано: , .

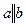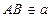Построить: М – середина АВ

Построение:

1) 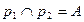- произвольно;

2) ;

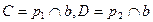3) ;

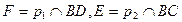4) 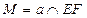- искомая точка.

Доказательство:

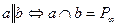. По теореме о полном четырёхвершиннике 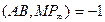, а по теореме 2 из §13 точка М – середина отрезка АВ.