172. Доказать, что в любом треугольнике: а) три медианы пересекаются в одной точке; б) каждая медиана точкой пересечения делится в отношении 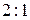 , считая от вершины.
, считая от вершины.
173. Доказать, что в произвольной трапеции точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на прямой, проходящей через середины оснований.
174. Точки 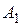 ,
, 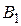 и
и 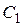 лежат на сторонах
лежат на сторонах 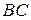 ,
, 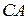 ,
, 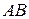 треугольника
треугольника 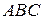 , причем
, причем 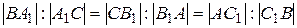 . Доказать, что центр тяжести треугольника
. Доказать, что центр тяжести треугольника 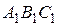 совпадает с центром тяжести треугольника
совпадает с центром тяжести треугольника  и что то же справедливо для центра тяжести треугольника, образованного при пересечении прямых
и что то же справедливо для центра тяжести треугольника, образованного при пересечении прямых  ,
, 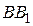 и
и 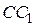 .
.
175. Каждая из сторон треугольника разделена на три равные части и каждая из точек деления соединена прямой с противоположной вершиной треугольника. Доказать, что в образованном этими прямыми шестиугольнике диагонали, соединяющие его противоположные вершины, пересекаются в одной точке.
176. Даны три попарно пересекающиеся прямые 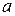 ,
, 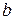 ,
, 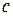 , не принадлежащие одному пучку, и точка
, не принадлежащие одному пучку, и точка 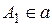 . Через точку
. Через точку 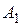 проведена прямая
проведена прямая 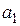 , параллельная прямой
, параллельная прямой 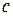 и пересекающая прямую
и пересекающая прямую 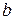 в точке
в точке 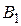 ; через точку
; через точку 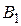 проведена прямая
проведена прямая 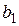 , параллельная прямой
, параллельная прямой 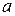 и пересекающая прямую
и пересекающая прямую 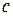 в точке
в точке 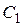 ; через точку
; через точку 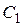 проведена прямая
проведена прямая 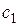 , параллельная прямой
, параллельная прямой 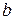 и пересекающая прямую
и пересекающая прямую 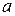 в точке
в точке 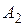 . Доказать, что либо точка
. Доказать, что либо точка 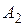 совпадает с точкой
совпадает с точкой 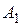 , либо (если
, либо (если 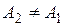 ) точка
) точка 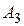 прямой
прямой 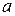 , полученная аналогичным построением, начатым с точки
, полученная аналогичным построением, начатым с точки 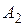 , совпадает с точкой
, совпадает с точкой 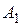 .
.
 2015-06-28
2015-06-28 492
492








