Задачи с применением инверсии

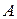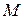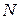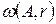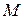177. Доказать, что если точки , , не лежат на одной прямой и в инверсии относительно окружности точки и 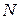преобразуются в точк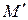и и 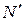, то около четырехугольника 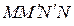можно описать окружность.

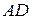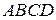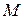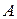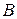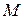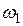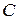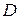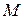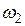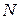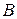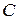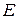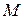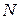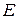178. На основании равнобедренной трапеции дана точка . Через точки , и проведена окружность , а через точки , и - окружность . Доказать, что вторая точка пересечения этих окружностей – точка , точки , и точка пересечения боковых сторон трапеции лежат на одной окружности, а точки , и лежат на одной прямой.

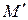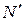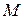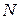179. Пусть точки и - образы точек и в инверсии 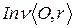. Доказать, что если точк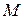и и 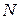не совпадают с центром 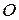инверсии, то имеет место равенство:

.

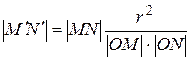180. Доказать, что для любых четырех точек 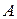, , 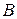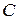и 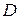, лежащих на одной прямой, имеет место соотношение:

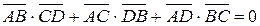
181. Доказать, что окружность (отличная от окружности инверсии) инвариантна в инверсии тогда и только тогда, когда она ортогонально пересекает окружность инверсии.

182. Пусть 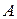, , 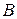, 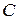– четыре точки, отличные от центра некоторой инверсии. Доказать, что в этой инверсии число 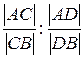является инвариантом.

183. Пусть инверсия с центром 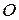переводит окружность 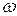в окружность 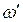. Доказать, что 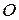– центр гомотетии, переводящей 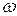в .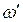

184. Найти расстояние между центром 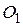окружности 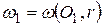, вписанной в некоторый треугольник 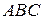, и центром 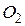окружности 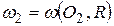, описанной около того же треугольника, если считать радиусы 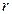и 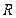этих окружностей известными.