Прямая линия в пространстве может принадлежать плоскости, а также быть параллельной плоскости или пересекать ее. При пересечении прямой линии с плоскостью следует выделить частный случай, когда прямая перпендикулярна плоскости.
Прямая линия, параллельная плоскости. Прямая линия параллельна плоскости, если она параллельна любой прямой принадлежащей этой плоскости. Поэтому, чтобы провести через заданную точку прямую, параллельную плоскости, надо сначала в плоскости провести произвольную прямую, а затем провести через точку искомую прямую, параллельную прямой, принадлежащей плоскости.


а
/b
/ êê c
/d
/

ab êê cd
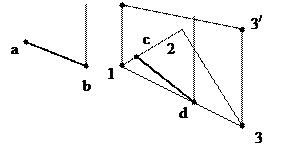
Прямая линия, пересекающая плоскость. Если прямая не принадлежит плоскости и не параллельна ей, то она пересекает данную плоскость. Задача на пересечение прямой линии с плоскостью является одной из основных задач начертательной геометрии.
При решении задач на пересечение прямой с плоскостью следует выделить частный случай. Если плоскость занимает проецирующее положение, то одна проекция точки пересечения определяется в пересечении проекции прямой с проецирующим следом плоскости, а другая проекция строится с помощью линии связи.

 X
X
Если заданная плоскость общего положения, то точка пересечения прямой с плоскостью определяется с помощью вспомогательной секущей плоскости.
Для построения точки пересечения прямой линии с плоскостью необходимо:
1) провести через прямую МN вспомогательную проецирующую плоскость S;
2) построить линию пересечения данной плоскости и вспомогательной;
3) определить искомую точку К пересечения данной прямой МN с линией пересечения плоскостей.
Решение задачи завершается определением видимых участков прямой. Видимость прямой относительно плоскости треугольника определяют путем разбора взаимоположения точек заданной прямой и сторон плоскости треугольника, совпадающих на проекциях.


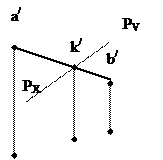
 а/b/ êê c/d/
а/b/ êê c/d/

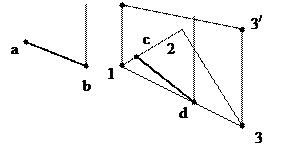

 X
X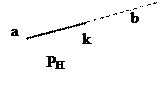
 2015-06-28
2015-06-28 569
569








