2015-06-28
512
Плоскости и прямые в пространстве.
Пусть заданы прямая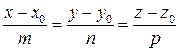 
и плоскость Ax+By+Cz+D=0.
Угол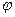 
между прямой и плоскостью определяется по формуле:
.
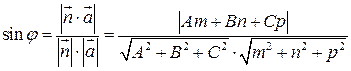Условия параллельности прямой и плоскости: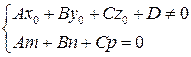 
Условие перпендикулярности прямой и плоскости: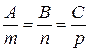 
.
Условия, при которых прямая принадлежит плоскости:
.
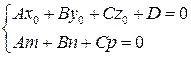Чтобы определить точку пересечения прямой и плоскости надо:
1) написать параметрические уравнения прямой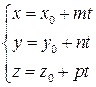 
;
2) подставить в уравнение плоскости Ax+By+Cz+D=0 вместо x,y,z их выражения через t и найти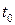 
;
3) из параметрических уравнений прямой, подставив в них 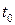, найти координаты точки пересечения.
Задачи для самостоятельного решения.
№1. Установите взаимное расположение прямой и плоскости:
а)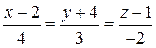 
и 5x-2y+7z+3=0;
б)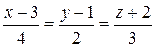 
и 2x-y-2z-9=0;
в)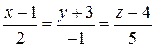 
и 3x-4y-2z-7=0;
г)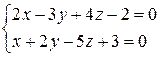 
и 2x-7y+12z-15=0.
№2. Вычислить угол между прямой и плоскостью:
а)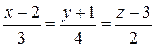 
и x+2y-3z+4=0;
б)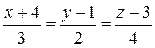 
и 2x-3y-2z+5=0.
----------------------------------------------------------------------------------------------------------------
Прямые и плоскости в пространстве. Стр.1
№3. Найти точку пересечения прямой и плоскости:
а)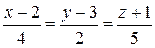 
и x+2y-3z-4=0;
б)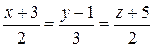 
и 2x+3y+z-22=0.
№4. Найти проекцию точки на плоскость:
|
|
|
а) А(3,-2,4), 2x+y+3z+12=0;
б) В(3,1,-1), x+2y+3z-30=0;
в) М(5,2,-1), 2x-y+3z+23=0.
№5. При каких значениях а и с прямая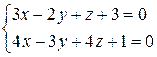 
перпендикулярна к плоскости аx+8y+сz+2=0?
№6. Составить уравнение плоскости, проходящей через начало координат и прямую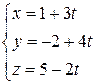 
.
№7. При каких значениях а и d прямая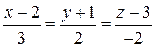 
лежит в плоскости аx+y-2z+d=0?
№8. Найти точку пересечения прямой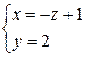 
и плоскости y=z, а также угол между ними.
№9. Написать уравнение плоскости, проходящей через прямую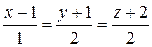 
и перпендикулярной к плоскости 2x+3y-z=4.
№10. Найти точку пересечения прямой, проходящей через точки А(0,0,4) и В(2,2,0), и плоскостью x+y-z=0, а также угол между ними.
№11. Написать уравнение плоскости, проходящей через прямую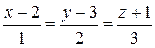 
и точку А(3,4,0).
----------------------------------------------------------------------------------------------------------------
Прямые и плоскости в пространстве. Стр.2
