Общее уравнение плоскости

Будем считать, что в пространстве задана некоторая ДПСК.

Определение. Всякий ненулевой вектор, перпендикулярный данной плоскости, называется ее нормальным вектором. Обозначение: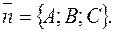

Теорема. В декартовых координатах всякая плоскость определяется уравнением первой степени, т.е. уравнением вида

Ax+By+Cz+D= 0. (1)

И обратно: всякое уравнение вида (1) определяет в пространстве некоторую плоскость.

Доказательство этой теоремы аналогично доказательству теоремы об общем уравнении прямой на плоскости.

Уравнение (1) называют общим уравнением плоскости. Коэффициенты A,B,C – это проекции нормального вектора плоскости.

Уравнение вида

A (x–x ₀) +B (y–y ₀) +C (z–z ₀) = 0

является уравнением плоскости, проходящей через точку M ₀(x ₀; y ₀; z ₀) и имеющей нормальный вектор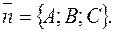

Пример. Составить уравнение плоскости α, проходящей через данную точку M ₀(1;2;3) и перпендикулярной плоскостям β:x+ 2 y–z= 0 и γ:2 x–y+ 3 z +1=0.

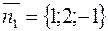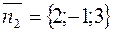Решение. Нормальные векторы и плоскостей β и γ перпендикулярны своим плоскостям, а значит параллельны плоскости α, т.к. 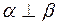и 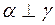. Но тогда векторное произведение 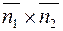, будучи перпендикулярным своим сомножителям, будет также перпендикулярным к плоскости 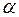, т.е. оно является нормальным вектором этой плоскости. Найдем его:

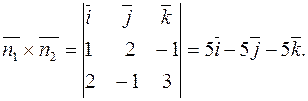
Вектор 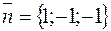, коллинеарный 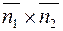, также будет нормальным вектором искомой плоскости α. Теперь можем составить ее уравнение:

1(x–1)+(–1)(y– 2)+(–1)(x– 3)=0 или

x–y–z+ 4=0.